题目内容
4.在区间[-1,3]内任选一个实数,则x恰好在区间[1,3]内的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 本题利用几何概型求概率,解得的区间长度,求比值即得.
解答 解:利用几何概型,其测度为线段的长度,
区间[-1,3]的长度为4,区间[1,3]长度为2,
由几何概型公式得x恰好在区间[1,3]内的概率是为$\frac{2}{4}$=$\frac{1}{2}$.
故选:C.
点评 本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
15.函数y=ax(a>0,且a≠1)在[0,1]上的最大值与最小值之和为3,则a=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
12.已知集合U={1,2,3,4,5,6,7},集合A={2,4,5},则∁UA=( )
| A. | ∅ | B. | {1,3,5} | C. | {1,3,6,7} | D. | {1,3,5,7} |
19.执行如图所示的程序框图,如果是输入的变量t∈[-2,-1],则输出的S属于( )
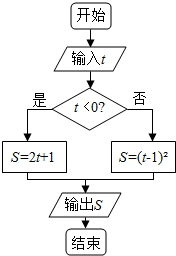

| A. | (-5,-3) | B. | [-3,-1] | C. | [4,9] | D. | [-3,4] |

 设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-a,x<1}\\{{x}^{2}-4ax+3{a}^{2},x≥1}\end{array}\right.$
设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-a,x<1}\\{{x}^{2}-4ax+3{a}^{2},x≥1}\end{array}\right.$