题目内容
5.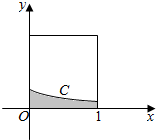 在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )附“若X~N(μ,σ2),则
P(μ-σ<X≤μ+σ)=0.6826.
p(μ-2σ<X≤μ+2σ)=0.9544.
| A. | 1193 | B. | 1359 | C. | 2718 | D. | 3413 |
分析 根据正态分布的定义,可以求出阴影部分的面积,也就是x在(0,1)的概率.
解答 解:正态分布的图象如下图: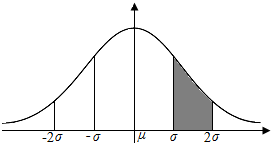
正态分布N(-1,1)则在(0,1)的概率如上图阴影部分,
其概率为$\frac{1}{2}$×[P(μ-2σ<X≤μ+2σ)-P(μ-σ<X≤μ+σ)]=$\frac{1}{2}$×(0.9544-0.6826)=0.1359;
即阴影部分的面积为0.1359;
所以点落入图中阴影部分的概率为p=$\frac{0.1359}{1}$=0.1359;
投入10000个点,落入阴影部分的个数期望为10000×0.1359=1359.
故选B.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量μ和σ的应用,考查曲线的对称性,属于基础题.

练习册系列答案
相关题目
15.已知命题p:存在x∈R,使tanx=$\frac{\sqrt{2}}{2}$,命题q:x2-3x+2<0的解集是{x|1<x<2},下列结论:
①命题“p且q”是真命题;
②命题“p且¬q”是假命题;
③命题“¬p或q”是真命题;
④命题“¬p或¬q”是假命题,
其中正确的是( )
①命题“p且q”是真命题;
②命题“p且¬q”是假命题;
③命题“¬p或q”是真命题;
④命题“¬p或¬q”是假命题,
其中正确的是( )
| A. | ②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
17.已知{an}是等差数列,a3=8,S6=57,则过点P(2,a7),Q(3,a8)的直线斜率为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | -13 |
15.函数y=ax(a>0,且a≠1)在[0,1]上的最大值与最小值之和为3,则a=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |