题目内容
设O是锐角△ABC的外心,若∠C=75°,且△AOB,△BOC,△COA的面积满足关系式S△AOB+S△BOC=
S△COA,求∠A.
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:根据C的度数,利用内角和定理用A表示出B,设圆O为△ABC外接圆,令圆O半径为r,可得OA=OB=OC=r,利用圆周角定理得到∠AOB=2∠C=150°,∠BOC=2∠A,∠COA=2∠B,分别表示出三角形AOB,三角形BOC,以及三角形COA的面积,代入已知等式,整理后求出cos2A的值,进而确定出A的度数,检验即可.
解答:
解:由题意得∠B=180°-∠A-∠C=105°-∠A,
设圆O为△ABC外接圆,令圆O半径为r,
∴OA=OB=OC=r,∠AOB=2∠C=150°,∠BOC=2∠A,∠COA=2∠B,
∴S△AOB=
OA•OB•sin∠AOB=
r2; S△BOC=
OB•OC•sin∠BOC=
r2sin2A; S△COA=
OC•OA•sin∠COA=
r2sin2B,
代入已知等式得:
r2+
r2sin2A=
×
r2sin2B,
整理得:1+2sin2A=2
sin2B=2
sin(210°-2A)=2
(sin210°cos2A-cos210°sin2A)=2
(
sin2A-
cos2A)=3sin2A-
cos2A,
即1+
cos2A=sin2A,
两边平方得:1+2
cos2A+3cos22A=sin22A=1-cos22A,
整理得:cos2A(
+2cos2A)=0,
可得cos2A=0或cos2A=-
,
∵△ABC为锐角三角形,∴0<∠A<90°,
∴0<2∠A<180°,
当cos2A=0时,2∠A=90°,即∠A=45°;
当cos2A=-
时,2∠A=150°,即∠A=75°,
由S△AOB+S△BOC=
S△COA等同于sin2C+sin2A=
sin2B,
当∠A=45°时,∠C=75°,∠B=60°,代入该条件,符合;
当∠A=75°时,∠C=75°,∠B=30°,代入该条件,不符合,舍去,
则∠A=45°.
设圆O为△ABC外接圆,令圆O半径为r,
∴OA=OB=OC=r,∠AOB=2∠C=150°,∠BOC=2∠A,∠COA=2∠B,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入已知等式得:
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
整理得:1+2sin2A=2
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
即1+
| 3 |
两边平方得:1+2
| 3 |
整理得:cos2A(
| 3 |
可得cos2A=0或cos2A=-
| ||
| 2 |
∵△ABC为锐角三角形,∴0<∠A<90°,
∴0<2∠A<180°,
当cos2A=0时,2∠A=90°,即∠A=45°;
当cos2A=-
| ||
| 2 |
由S△AOB+S△BOC=
| 3 |
| 3 |
当∠A=45°时,∠C=75°,∠B=60°,代入该条件,符合;
当∠A=75°时,∠C=75°,∠B=30°,代入该条件,不符合,舍去,
则∠A=45°.
点评:此题考查了三角形的面积公式,三角形外心性质,两角和与差的正弦函数公式,熟练掌握三角形的面积公式是解本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
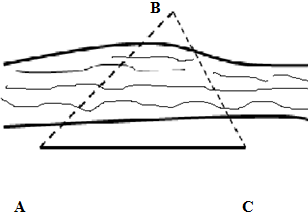 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.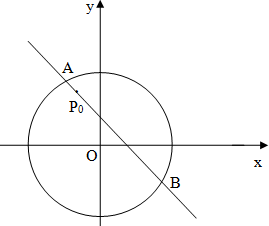 如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.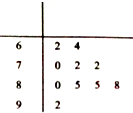 为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.
为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.