题目内容
14．若x，y∈R，且f（x+y）=f（x）+f（y），则函数f（x）（ ）| A． | f（0）=0且f（x）为偶函数 | B． | f（0）=0且f（x）为奇函数 | ||
| C． | f（x）为增函数且为奇函数 | D． | f（x）为增函数且为偶函数 |
分析 利用赋值法，即可得出结论．
解答 解：由题意，f（0+0）=f（0）+f（0），∴f（0）=0，
f（-x+x）=f（-x）+f（x）=0，∴f（x）为奇函数，
故选B．
点评 本题考查奇函数的定义与性质，考查学生的计算能力，比较基础．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
4．设等比函数{an}的前n项和为Sn，若$\frac{{S}_{6}}{{S}_{3}}$=3，则$\frac{{S}_{12}}{{S}_{9}}$=（ ）
| A． | $\frac{7}{3}$ | B． | $\frac{15}{7}$ | C． | $\frac{17}{7}$ | D． | $\frac{8}{3}$ |
9．设集合U={-1，-2，-3，-4，0}，集合A={-1，-2，0}，集合B={-3，-4，0}则（∁UA）∩B=（ ）
| A． | {-3，-4} | B． | {-1，-2} | C． | {0} | D． | ∅ |
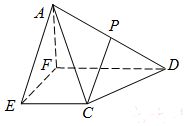如图，在四棱锥A-CDFE中，底面CDFE是直角梯形，CE∥DF，EF⊥EC，$CE=\frac{1}{2}DF$，AF⊥平面CDFE，P为AD中点．
