题目内容
4.已知抛物线y2=16x的焦点恰好是双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,则双曲线的渐近线方程为y=±$\frac{\sqrt{3}}{3}$x.分析 根据题意,求出抛物线y2=16x的焦点坐标,可得双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点坐标,进而可得12+b2=16,解可得b的值,由a、b的值结合双曲线渐近线方程计算可得答案.
解答 解:根据题意,抛物线的标准方程:y2=16x,其焦点坐标为(4,0),
则双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点坐标为(4,0),则c=4,
有12+b2=16,解可得b=2,
则双曲线的方程为$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1,
则该双曲线的渐近线方程y=±$\frac{\sqrt{3}}{3}$x;
故答案为:y=±$\frac{\sqrt{3}}{3}$x.
点评 本题考查双曲线的几何性质,涉及抛物线的标准方程,注意要先求出抛物线的焦点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若x,y∈R,且f(x+y)=f(x)+f(y),则函数f(x)( )
| A. | f(0)=0且f(x)为偶函数 | B. | f(0)=0且f(x)为奇函数 | ||
| C. | f(x)为增函数且为奇函数 | D. | f(x)为增函数且为偶函数 |
16.执行如图所示的程序框图,则输出y的值为( )
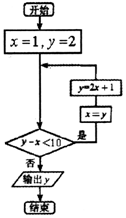

| A. | 5 | B. | 11 | C. | 23 | D. | 47 |
13.如果直线x=ky-1与圆C:x2+y2+kx+my+2p=0相交,且两个交点关于直线y=x对称,那么实数p的取值范围是( )
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{4}})$ | C. | $({-\frac{3}{4},+∞})$ | D. | $({-\frac{3}{2},+∞})$ |
3.已知函数f(x)=log3x,x0∈[1,27],则不等式1≤f(x0)≤2成立的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{13}$ | D. | $\frac{2}{9}$ |