题目内容
17.若|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,|$\overrightarrow{c}$|=$\sqrt{3}$,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$的最大值是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 求出|$\overrightarrow{a}+\overrightarrow{b}$|,根据数量积的定义即可得出最大值.
解答 解:($\overrightarrow{a}+\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=3,
∴|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$,
∴$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$=($\overrightarrow{a}+\overrightarrow{b}$)$•\overrightarrow{c}$=|$\overrightarrow{a}+\overrightarrow{b}$||$\overrightarrow{c}$|cosθ≤|$\overrightarrow{a}+\overrightarrow{b}$||$\overrightarrow{c}$|=3.
故选:D.
点评 本题考查了平面向量的数量积运算,属于中档题.

练习册系列答案
相关题目
8.按如图所示的程序框图,若输入a=81,则输出的i=( )
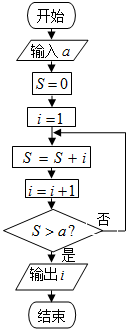

| A. | 14 | B. | 17 | C. | 19 | D. | 21 |
12.已知全集U=R,集合A={x|-3≤x≤1},集合B=$\left\{{x\left|{{2^x}<\frac{1}{4}}\right.}\right\}$,则A∩(∁UB)=( )
| A. | {x|-2<x<1} | B. | {x|-3≤x<-2} | C. | {x|-2≤x≤1} | D. | {x|-3≤x≤-2} |
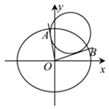 如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.
如图所示,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为$\frac{4\sqrt{3}}{3}$.