题目内容
20.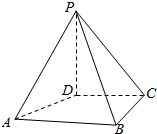 如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.(1)求∠ADC;
(2)求证:BC⊥PC;
(3)求点A到平面PBC的距离.
分析 (1)过D作BC的平行线DE,交AB于E,由已知能求出∠DAE=45°,从而能求出∠ADC.
(2)推导出PD⊥BC,BC⊥DC,由此能证明PC⊥BC.
(3)连结AC,设点A到平面PBC的距离为h,由等体积法能求出点A到平面PBC的距离.
解答 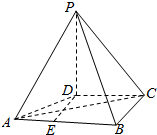 解:(1)过D作BC的平行线DE,交AB于E,
解:(1)过D作BC的平行线DE,交AB于E,
∵在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,
∴AE=DE=1,DE⊥AE,
∴∠DAE=45°,
∴∠ADC=135°.
证明:(2)∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥BC,
由∠BCD=90°,得BC⊥DC,
又PD∩DC=D,PD?平面PCD,DC?平面PCD,
∴BC⊥平面PCD,
∵PC?平面PCD,
∴PC⊥BC.
解:(3)连结AC,设点A到平面PBC的距离为h,
因为AB∥DC,∠BCD=90°,所以∠ABC=90°,
从而由AB=2,BC=1,得△ABC的面积S△ABC=1,
由PD⊥平面ABCD及PD=1,
得三棱锥P-ABC的体积V=$\frac{1}{3}{S}_{△ABC}•PD=\frac{1}{3}$,
∵PD⊥平面ABCD,DC?平面ABCD,
∴PD⊥DC,
又PD=DC=1,∴PC=$\sqrt{P{D}^{2}+D{C}^{2}}$=$\sqrt{2}$,
由PC⊥BC,BC=1,得△PBC的面积S△PBC=$\frac{\sqrt{2}}{2}$,
由$V=\frac{1}{3}{S}_{△PBC}h$=$\frac{1}{3}•\frac{\sqrt{2}}{2}•h$=$\frac{1}{3}$,解得h=$\sqrt{2}$,
∴点A到平面PBC的距离为$\sqrt{2}$.
点评 本题考查角的求法,考查线线垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=1,则下列结论中错误的是( )
如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=1,则下列结论中错误的是( )| A. | EF∥平面ABCD | B. | AC⊥BE | ||
| C. | 三棱锥A-BEF体积为定值 | D. | △BEF与△AEF面积相等 |
| A. | $\left\{\begin{array}{l}{x={t}^{2}+1}\\{y=0}\end{array}\right.$(t为参数) | B. | $\left\{\begin{array}{l}{x=0}\\{y=3t+1}\end{array}\right.$(t为参数) | ||
| C. | $\left\{\begin{array}{l}{x=1+sinθ}\\{y=0}\end{array}\right.$(θ为参数) | D. | $\left\{\begin{array}{l}{x=4t+1}\\{y=0}\end{array}\right.$(t为参数) |
| A. | 5,10,15,20,25 | B. | 2,4,8,16,32 | C. | 5,6,7,8,9 | D. | 6,16,26,36,46 |
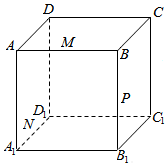 如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.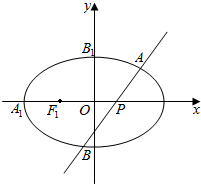 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,|A1B1|=$\sqrt{7}$,F1是椭圆C的左焦点,A1是椭圆C的左顶点,B1是椭圆C的上顶点,且$\overrightarrow{{A}_{1}{F}_{1}}$=$\overrightarrow{{F}_{1}O}$,点P(n,0)(n≠0)是长轴上的任一定点,过P点的任一直线l交椭圆C于A,B两点.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,|A1B1|=$\sqrt{7}$,F1是椭圆C的左焦点,A1是椭圆C的左顶点,B1是椭圆C的上顶点,且$\overrightarrow{{A}_{1}{F}_{1}}$=$\overrightarrow{{F}_{1}O}$,点P(n,0)(n≠0)是长轴上的任一定点,过P点的任一直线l交椭圆C于A,B两点.