题目内容
13.函数$y=sin({\frac{π}{3}x+\frac{π}{6}})$的图象可由函数$y=cos\frac{π}{3}x$的图象至少向右平移m(m>0)个单位长度得到,则m=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
分析 利用诱导公式,y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:函数$y=sin({\frac{π}{3}x+\frac{π}{6}})$=cos[$\frac{π}{2}$-($\frac{π}{3}$x+$\frac{π}{6}$)]=cos$\frac{π}{3}$(x-1)的图象可由函数$y=cos\frac{π}{3}x$的图象
至少向右平移1个单位长度得到,
又函数$y=sin({\frac{π}{3}x+\frac{π}{6}})$的图象可由函数$y=cos\frac{π}{3}x$的图象
至少向右平移m(m>0)个单位长度得到,
∴m=1,
故选:A.
点评 本题主要考查诱导公式,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
1.若执行如图所示的程序框图,则输出的结果k=( )
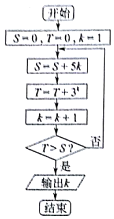

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.下表是某校高三一次月考5个班级的数学、物理的平均成绩:
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| 班级 | 1 | 2 | 3 | 4 | 5 |
| 数学(x分) | 111 | 113 | 119 | 125 | 127 |
| 物理(y分) | 92 | 93 | 96 | 99 | 100 |
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
5.执行如图所示的程序框图,若输入的n=5,则输出的结果为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
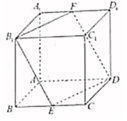 在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.