题目内容
13. 在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.(1)求证:四边形B1EDF是菱形;
(2)求异面直线A1C与DE所成的角 (结果用反三角函数表示).
分析 (1)由题意画出图形,取AD中点G,连接FG,BG,可证四边形B1BGF为平行四边形,得BG∥B1F,再由ABCD-A1B1C1D1为正方体,且E,G分别为BC,AD的中点,可得BEDG为平行四边形,得BG∥DE,BG=DE,从而得到B1F∥DE,且B1F=DE,进一步得到四边形B1EDF为平行四边形,再由△B1BE≌△B1A1F,可得B1E=B1F,得到四边形B1EDF是菱形;
(2)以A为原点建立如图所示空间直角坐标系,然后利用空间向量求异面直线A1C与DE所成的角.
解答 (1)证明: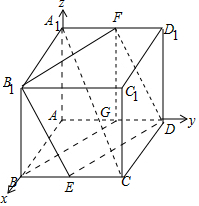
取AD中点G,连接FG,BG,可得B1B∥FG,B1B=FG,
∴四边形B1BGF为平行四边形,则BG∥B1F,
由ABCD-A1B1C1D1为正方体,且E,G分别为BC,AD的中点,
可得BEDG为平行四边形,∴BG∥DE,BG=DE,
则B1F∥DE,且B1F=DE,
∴四边形B1EDF为平行四边形,由△B1BE≌△B1A1F,可得B1E=B1F,
∴四边形B1EDF是菱形;
(2)解:以A为原点建立如图所示空间直角坐标系,
设正方体的棱长为1,则A1(0,0,1),C(1,1,0),D(0,1,0),E(1,$\frac{1}{2}$,0),
∴$\overrightarrow{{A}_{1}C}=(1,1,-1)$,$\overrightarrow{DE}=(1,-\frac{1}{2},0)$,
∴cos<$\overrightarrow{{A}_{1}C},\overrightarrow{DE}$>=$\frac{\overrightarrow{{A}_{1}C}•\overrightarrow{DE}}{|\overrightarrow{{A}_{1}C}|•|\overrightarrow{DE}|}$=$\frac{\frac{1}{2}}{\sqrt{3}×\frac{\sqrt{5}}{2}}=\frac{\sqrt{15}}{15}$.
∴异面直线A1C与DE所成的角为arccos$\frac{\sqrt{15}}{15}$.
点评 本题考查空间中直线与直线的位置关系,考查空间想象能力和思维能力,训练了利用空间向量求异面直线所成角,是中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | {x|0≤x≤3} | B. | {1,2,3} | C. | {0,1,2,3} | D. | {x|1≤x≤3} |
市民参加广场活动项目与性别列联表
| 广场舞 | 球、棋、牌 | 总计 | |
| 男 | 100 | 200 | 300 |
| 女 | 300 | 400 | 700 |
| 总计 | 400 | 600 | 1000 |
(Ⅱ)以性别为标准,用分层抽样的方法在跳广场舞的人员中抽取4人,再在这4人中随机确定两名做广场舞管理,求这两名管理是一男一女的概率.
附 参考公式和K2检验临界值表:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d,
| P(K2≥k | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |