Question

20．设x，y满足约束条件$\left\{\begin{array}{l}{8x-y-4≤0}\\{x+y+1≥0}\\{y-4x≤0}\end{array}\right.$，目标函数z=ax+by（a＞0，b＞0）的最大值为2，
（1）求a+4b的值．
（2）求$\frac{1}{a}$+$\frac{1}{b}$的最小值．

Answer 1

分析 （1）画出不等式组表示的平面区域，找出最优解，计算目标函数的最大值；
（2）由题意，利用基本不等式计算$\frac{1}{a}$+$\frac{1}{b}$的最小值．

解答 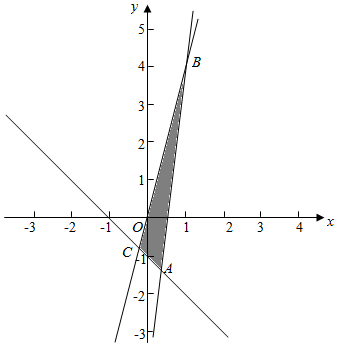解：（1）不等式组$\left\{\begin{array}{l}{8x-y-4≤0}\\{x+y+1≥0}\\{y-4x≤0}\end{array}\right.$表示的平面区域
如图所示阴影部分，
当直线ax+by=z（a＞0，b＞0）过直线8x-y-4=0与y=4x的交点B（1，4）时，
目标函数z=ax+by（a＞0，b＞0）取得最大2，
即a+4b=2；…（6分）
（2）由题意，$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{2}$（a+4b）（$\frac{1}{a}$+$\frac{1}{b}$）
=$\frac{1}{2}$（5+$\frac{4b}{a}$+$\frac{a}{b}$）≥$\frac{1}{2}$（5+4）=$\frac{9}{2}$；
当且仅当a=2b=$\frac{2}{3}$时等号成立，
所以$\frac{1}{a}$+$\frac{1}{b}$的最小值是$\frac{9}{2}$．…（12分）

点评 本题考查了简单的线性规划问题，也考查了利用基本不等式求最值的应用问题，是中档题．