题目内容
已知双曲线E:
-
=1(a>0)的中心为原点O,左、右焦点分别为F1、F2,离心率为
,点P是直线x=
上任意一点,点Q在双曲线E上,且满足
•
=0.
(1)求实数a的值;
(2)证明:直线PQ与直线OQ的斜率之积是定值.
| x2 |
| a2 |
| y2 |
| 4 |
3
| ||
| 5 |
| a2 |
| 3 |
| PF2 |
| QF2 |
(1)求实数a的值;
(2)证明:直线PQ与直线OQ的斜率之积是定值.
考点:直线与圆锥曲线的关系
专题:计算题,证明题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由离心率公式和双曲线的a,b,c的关系,即可求得a;
(2)设出P(
,m),设Q(x0,y0),代入双曲线的方程,再由
•
=0,得到方程,再由直线的斜率公式,得到直线PQ与直线OQ的斜率之积,化简整理,运用代入,即可得到定值
.
(2)设出P(
| 5 |
| 3 |
| PF2 |
| QF2 |
| 4 |
| 5 |
解答:
(1)解:双曲线E:
-
=1(a>0)的b=2,c2=a2+4,
由于离心率为
,即e=
=
,
即有
=
,解得,a=
;
(2)证明:由于点P是直线x=
上任意一点,可设P(
,m),
再由Q为双曲线
-
=1一点,可设Q(x0,y0),
则
-
=1,即y02=4(
-1).
由F2(3,0),
则
•
=(
,-m)•(3-x0,-y0)=0,
即有4-
x0+my0=0,即有my0=-4+
x0,
则kPQ•kOQ=
•
=
=
=
=
.
则直线PQ与直线OQ的斜率之积是定值.
| x2 |
| a2 |
| y2 |
| 4 |
由于离心率为
3
| ||
| 5 |
| c |
| a |
3
| ||
| 5 |
即有
| a2+4 |
| a2 |
| 9 |
| 5 |
| 5 |
(2)证明:由于点P是直线x=
| 5 |
| 3 |
| 5 |
| 3 |
再由Q为双曲线
| x2 |
| 5 |
| y2 |
| 4 |
则
| x02 |
| 5 |
| y02 |
| 4 |
| x02 |
| 5 |
由F2(3,0),
则
| PF2 |
| QF2 |
| 4 |
| 3 |
即有4-
| 4 |
| 3 |
| 4 |
| 3 |
则kPQ•kOQ=
| m-y0 | ||
|
| y0 |
| x0 |
| my0-y02 | ||
x0(
|
=
| ||||
x0(
|
| ||||
x0(
|
| 4 |
| 5 |
则直线PQ与直线OQ的斜率之积是定值.
点评:本题考查双曲线的方程和性质,考查平面向量的数量积的坐标公式,考查直线的斜率公式的运用,考查化简整理的运算能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
在空间直角坐标系O-xyz中,点(-2,0,4)关于y轴的对称点是( )
| A、(-2,0,-4) |
| B、(2,0,-4) |
| C、(4,0,-2) |
| D、(2,0,4) |
函数g(x)=4×3x的图象可看成将函数f(x)=3x的图象( )
| A、向左平移log34个单位得到 | ||
| B、各点横坐标不变,纵坐标伸长的原来的4倍得到 | ||
| C、向右平移log34个单位得到 | ||
D、各点纵坐标不变,横坐标缩短的原来的
|
已知函数f(x)=
,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则x3(x1+x2)+
的取值范围是( )
|
| 1 | ||
|
| A、(-1,+∞) |
| B、(-1,1] |
| C、(-∞,1) |
| D、[-1,1) |
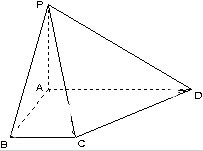 如图所示,已知ABCD是直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,P是平面ABCD外的一点,PA⊥平面ABCD,且PA=a,求点A到平面PCD的距离.
如图所示,已知ABCD是直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,P是平面ABCD外的一点,PA⊥平面ABCD,且PA=a,求点A到平面PCD的距离.