题目内容
从6双不同手套中,任取4只.
(1)恰有1双配对的取法是多少?
(2)没有1双配对的取法是多少?
(3)至少有一双配对的取法是多少?
(1)恰有1双配对的取法是多少?
(2)没有1双配对的取法是多少?
(3)至少有一双配对的取法是多少?
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:(1)可以分三步用分步乘法计数原理求得;
(2)求出从6双不同手套中,任取4只,共有
=495种方法,2双配对的取法是
=15种方法,利用间接法,可得没有1双配对的取法;
(3)至少有一双配对,包括恰有1双配对、2双配对,即可求出至少有一双配对的取法.
(2)求出从6双不同手套中,任取4只,共有
| C | 4 12 |
| C | 2 6 |
(3)至少有一双配对,包括恰有1双配对、2双配对,即可求出至少有一双配对的取法.
解答:
解:(1)分步解决:从6双中选出一双同色的手套,有6种方法;从剩下的十只手套中任选一只,有10种方法;
从除前所涉及的两双手套之外的八只手套中任选一只,有8种方法;由于选取与顺序无关,因而共有6×10×8÷2=240种.
(2)从6双不同手套中,任取4只,共有
=495种方法,2双配对的取法是
=15种方法,∴没有1双配对的取法是495-240-15=240种;
(3)至少有一双配对,包括恰有1双配对、2双配对,故至少有一双配对的取法是240+15=255种方法
从除前所涉及的两双手套之外的八只手套中任选一只,有8种方法;由于选取与顺序无关,因而共有6×10×8÷2=240种.
(2)从6双不同手套中,任取4只,共有
| C | 4 12 |
| C | 2 6 |
(3)至少有一双配对,包括恰有1双配对、2双配对,故至少有一双配对的取法是240+15=255种方法
点评:本题考查排列、组合与分步计数原理,考查间接法,解决的重点在于分步.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知函数f(x)=
那么f(
)的值为( )
|
| 4 |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
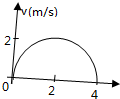 如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )
如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )| A、物体前2s作匀加速直线运动,后2s作匀减速直线运动 |
| B、物体在前2s作加速度越来越小的加速运动,后2s作加速度越来越大的减速运动 |
| C、物体在4s内的位移大小是2π(m) |
| D、物体在4s内的位移大小无法确定 |