题目内容
4. 如图所示的多面体ABCDEF,四边形ABCD是边长为2的正方形,面BDFE⊥面ABCD,四边形BDFE为矩形,BE长为a,M为AE的中点,AC∩BD=O.
如图所示的多面体ABCDEF,四边形ABCD是边长为2的正方形,面BDFE⊥面ABCD,四边形BDFE为矩形,BE长为a,M为AE的中点,AC∩BD=O.(1)求证:OM∥平面ADF;
(2)若BF⊥AE,求三棱锥E-BOM的体积.
分析 (1)取AF中点N,连接MN,DN,由三角形中位线定理及平行公理可得四边形MNDO为平行四边形,则OM∥ND,再由线面平行的判定可得OM∥平面ADF;
(2)由面BDEF⊥面ABCD,正方形ABCD中AC⊥BD,可得AC⊥平面BDEF,则AC⊥BF,再由BF⊥AE,得BF⊥OE,求得a=2,然后利用等积法求三棱锥E-BOM的体积.
解答 (1)证明:取AF中点N,连接MN,DN,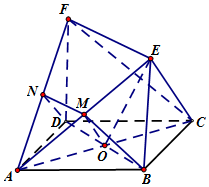
∵M为AE的中点,
则$MN∥EF,MN=\frac{1}{2}EF,OD∥EF,OD=\frac{1}{2}EF$,
∴MN∥OD,MN=OD,
∴四边形MNDO为平行四边形,
∴OM∥ND,
∵ND?平面ADF,OM?平面ADF,
∴OM∥平面ADF;
(2)解:∵面BDEF⊥面ABCD,正方形ABCD中AC⊥BD,
∴AC⊥平面BDEF,则AC⊥BF,
若BF⊥AE,则BF⊥平面ACE,BF⊥OE,
在矩形BDEF中,得a=2,
∴${V_{E-BOM}}={V_{A-BOM}}={V_{M-AOB}}=\frac{1}{3}×\frac{1}{2}×AO×BO×\frac{BE}{2}=\frac{1}{3}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
14.已知在平面直角坐标系xoy中,直线x-ky+2k-1=0与圆x2+y2=4交于A,B两点,若在该圆上还存在一点C,使得$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$成立,则实数k的值为( )
| A. | 0 | B. | $\frac{4}{3}$ | C. | 0或$\frac{4}{3}$ | D. | 0或$-\frac{4}{3}$ |
15.要使圆x2+y2+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧,则有( )
| A. | D2+E2-4F>0,且F<0 | B. | D<0,F>0 | ||
| C. | D≠0,F≠0 | D. | F<0 |
12.已知函数y=f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,f(x)的导函数为f′(x)且当x>0时,xf′(x)-2f(x)<0,则一定成立的是( )
| A. | 16f(-3)>9f(4) | B. | 16f(3)<9f(-4) | C. | 9f(3)>16f(4) | D. | 9f(-3)<16f(-4) |
9.设点P(x,y) 在函数y=4-2x的图象上运动,则9x+3y的最小值为( )
| A. | 9 | B. | 12 | C. | 18 | D. | 22 |
 在四边形ABCD中,已知BC=2,DC=4,且∠A:∠ABC:∠C:∠ADC=3:7:4:10
在四边形ABCD中,已知BC=2,DC=4,且∠A:∠ABC:∠C:∠ADC=3:7:4:10