题目内容
20.在极坐标系中,曲线C的方程为$ρ=4cosθ+2sinθ-\frac{3}{ρ}$,以极点O为原点,极轴为x轴的正半轴建立平面直角坐标系.(Ⅰ)求曲线C的参数方程;
(Ⅱ)在直角坐标系中,点M(x,y)是曲线C上一动点,求x+y的最大值,并求此时点M的直角坐标.
分析 (Ⅰ)首先把曲线转化为:ρ2=4ρcosθ+2ρsinθ-3,整理得:(x-2)2+(y-1)2=2.进一步转化为参数方程为:$\left\{\begin{array}{l}{x=2+\sqrt{2}cosθ}\\{y=1+\sqrt{2}sinθ}\end{array}\right.$(θ为参数).
(Ⅱ)根据(Ⅰ)所得的参数方程,进一步利用三角函数的恒等变换变换成正弦型三角函数,最后求出函数关系式的最值及坐标.
解答 解:(Ⅰ)曲线C的方程为$ρ=4cosθ+2sinθ-\frac{3}{ρ}$,转化为:ρ2=4ρcosθ+2ρsinθ-3,
整理得:(x-2)2+(y-1)2=2.
进一步转化为参数方程为:$\left\{\begin{array}{l}{x=2+\sqrt{2}cosθ}\\{y=1+\sqrt{2}sinθ}\end{array}\right.$(θ为参数).
(Ⅱ)由(Ⅰ)得:
x+y=$3+\sqrt{2}(sinθ+cosθ)$,
=$3+2sin(θ+\frac{π}{4})$,
当且仅当$θ=\frac{π}{4}$时,(x+y)max=5.
M(3,2)为取得最大值时的坐标.
点评 本题考查的知识点:极坐标方程与参数方程和普通方程的互化,三角函数关系式的恒等变换,三角函数的最值,属于基础题型.

练习册系列答案
相关题目
11.若f(x)的图象如图所示,则有( )


| A. | 0<f'(3)<f'(4)<f(4)-f(3) | B. | 0<f(4)-f(3)<f'(3)<f'(4) | C. | 0<f'(4)<f'(3)<f(4)-f(3) | D. | 0<f'(4)<f(4)-f(3)<f'(3) |
15.要使圆x2+y2+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧,则有( )
| A. | D2+E2-4F>0,且F<0 | B. | D<0,F>0 | ||
| C. | D≠0,F≠0 | D. | F<0 |
12.已知函数y=f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,f(x)的导函数为f′(x)且当x>0时,xf′(x)-2f(x)<0,则一定成立的是( )
| A. | 16f(-3)>9f(4) | B. | 16f(3)<9f(-4) | C. | 9f(3)>16f(4) | D. | 9f(-3)<16f(-4) |
9.设点P(x,y) 在函数y=4-2x的图象上运动,则9x+3y的最小值为( )
| A. | 9 | B. | 12 | C. | 18 | D. | 22 |
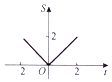
 在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )
在函数y=|x|(x∈[-2,2])的图象上有一点P(t,|t|),此函数的图象与x轴、直线x=-2及x=t围成的图形(如图阴影部分)的面积为S,则S与t的函数关系可表示为( )