题目内容
 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 6 |
(1)求椭圆E的标准方程.
(2)圆O是以椭圆E的长轴为直径的圆,M是直线x=-4在x轴上方的一点,过M点作圆O的两条切线,切点分别为P,Q,当∠PMQ=60°时,试证明点M关于直线PQ的对称点在圆O上.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆E的标准方程.
(2)连接OM,OP,OQ,设M(-4,m),由圆的切线性质及∠PMQ=60°,可知△OPM为直角三角形且∠OMP=30°,从而可求M(-4,4),进而以OM为直径的圆K的方程为(x+2)2+(y-2)2=8与圆O:x2+y2=8联立,两式相减可得直线PQ的方程.由此能证明点M关于直线PQ的对称点在圆O上.
|
(2)连接OM,OP,OQ,设M(-4,m),由圆的切线性质及∠PMQ=60°,可知△OPM为直角三角形且∠OMP=30°,从而可求M(-4,4),进而以OM为直径的圆K的方程为(x+2)2+(y-2)2=8与圆O:x2+y2=8联立,两式相减可得直线PQ的方程.由此能证明点M关于直线PQ的对称点在圆O上.
解答:
(1)解:∵椭圆E:
+
=1(a>b>0)的离心率e=
,
且经过点(
,1),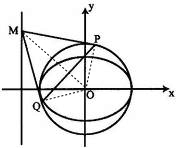
∴
,解得a2=8,b2=4,c2=4,
∴椭圆E的标准方程为
+
=1.
(2)证明:连接OM,OP,OQ,设M(-4,m)
由圆的切线性质及∠PMQ=60°,
知△OPM为直角三角形且∠OMP=30°,
∵|OP|=2
,∴|OM|=4
,
∴
=4
,∵m>0,∴m=4,
∴M(-4,4),
∴以OM为直径的圆K的方程为(x+2)2+(y-2)2=8
与圆O:x2+y2=8联立,两式相减可得直线PQ的方程为:x-y+2=0.
|OM|=
=4
,O到直线PQ的距离d=
=
,
∴M到直线PQ的距离4
-
=3
,
∴点M关于直线PQ的对称点到直线PQ的距离为3
,
∵圆O的半径r=2
,O到直线PQ的距离为
,
∴点M关于直线PQ的对称点在圆O上.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
且经过点(
| 6 |

∴
|
∴椭圆E的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)证明:连接OM,OP,OQ,设M(-4,m)
由圆的切线性质及∠PMQ=60°,
知△OPM为直角三角形且∠OMP=30°,
∵|OP|=2
| 2 |
| 2 |
∴
| 16+m2 |
| 2 |
∴M(-4,4),
∴以OM为直径的圆K的方程为(x+2)2+(y-2)2=8
与圆O:x2+y2=8联立,两式相减可得直线PQ的方程为:x-y+2=0.
|OM|=
| 16+16 |
| 2 |
| |2| | ||
|
| 2 |
∴M到直线PQ的距离4
| 2 |
| 2 |
| 2 |
∴点M关于直线PQ的对称点到直线PQ的距离为3
| 2 |
∵圆O的半径r=2
| 2 |
| 2 |
∴点M关于直线PQ的对称点在圆O上.
点评:本题以椭圆的性质为载体,考查椭圆的标准方程,考查圆与椭圆的综合,解题的关键是确定M的坐标,进而确定以OM为直径的圆K的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)(x∈R)满足f(1)=1,且f(x)在R上的导函数f′(x)<
,则不等式f(lgx)<
的解为( )
| 1 |
| 2 |
| lgx+1 |
| 2 |
| A、(10,+∞) |
| B、(1,+∞) |
| C、(0,1) |
| D、(1,+10) |
已知实数x、y满足条件:
,则z=|x+1|+|y-1|的取值范围是( )
|
| A、[1,3) |
| B、[0,4) |
| C、[1,4) |
| D、[0,3) |
角α的顶点在坐标原点O,始边在y轴的正半轴上,终边与单位圆交于第三象限内的点P,且tanα=-
;角β的顶点在坐标原点O,始边在x轴的正半轴上,终边与单位圆交于第二象限内的点Q,且tanβ=-2.对于下列结论:
①P(-
,-
);
②|PQ|2=
;
③cos∠POQ=-
;
④△POQ的面积为
,
其中正确结论的编号是( )
| 3 |
| 4 |
①P(-
| 3 |
| 5 |
| 4 |
| 5 |
②|PQ|2=
10+2
| ||
| 5 |
③cos∠POQ=-
| 3 |
| 5 |
④△POQ的面积为
| ||
| 5 |
其中正确结论的编号是( )
| A、①②③④ | B、②③④ |
| C、①③④ | D、①②④ |
| ∫ | 1 0 |
| A、e+cos1-2 |
| B、e+cos1 |
| C、e-2 |
| D、e-cos1 |
 已知如图长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,E是上底面中心,F,M为A1B1与CD的中点.
已知如图长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,E是上底面中心,F,M为A1B1与CD的中点. 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AB,点M、N分别在棱PD、PC上,且PC⊥平面AMN.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AB,点M、N分别在棱PD、PC上,且PC⊥平面AMN.