题目内容
 已知如图长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,E是上底面中心,F,M为A1B1与CD的中点.
已知如图长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,E是上底面中心,F,M为A1B1与CD的中点.(Ⅰ)写出C1M与平面EFAD的位置关系并证明.
(Ⅱ)求证:平面B1BAF⊥平面EFAD.
(Ⅲ)求几何体B1EF-BDA的表面积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)C1M∥平面EFAD.由已知条件条件出C1M∥AF,由此能证明C1M∥平面EFAD.
(Ⅱ)由已知条件推导出AD⊥平面B1BAF,由此能证明B1BAF⊥平面EFAD.
(Ⅲ)几何体B1EF-BDA的表面积:S=S梯形ADEF+S梯形BDEB1+S梯形ABB1F+S△B1EF+S△ABD,由此能示出结果.
(Ⅱ)由已知条件推导出AD⊥平面B1BAF,由此能证明B1BAF⊥平面EFAD.
(Ⅲ)几何体B1EF-BDA的表面积:S=S梯形ADEF+S梯形BDEB1+S梯形ABB1F+S△B1EF+S△ABD,由此能示出结果.
解答:
(Ⅰ)解:C1M∥平面EFAD.证明如下:
由题意知A1F∥CM,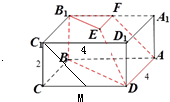 AA1∥CC1,
AA1∥CC1,
又CC1∩CM=C,∴面CC1M∥面A1AF,
又C1M与AF共面,∴C1M∥AF,
∵AF?平面EFAD,C1M不包含于平面EFAD,
∴C1M∥平面EFAD.
(Ⅱ)证明:∵长方体ABCD-A1B1C1D1中,
AD⊥平面AA1B1B,即AD⊥平面B1BAF,
又AD?平面EFAD,
∴平面B1BAF⊥平面EFAD.
(Ⅲ)解:∵AB=AD=2AA1=4,
E是上底面中心,F,M为A1B1与CD的中点,
∴几何体B1EF-BDA的表面积:
S=S梯形ADEF+S梯形BDEB1+S梯形ABB1F+S△B1EF+S△ABD
=
(2+4)•
+
(2
+4
)•2+
(2+4)•2+
×2×2+
×4×4
=3
+6
+16.
由题意知A1F∥CM,
 AA1∥CC1,
AA1∥CC1,又CC1∩CM=C,∴面CC1M∥面A1AF,
又C1M与AF共面,∴C1M∥AF,
∵AF?平面EFAD,C1M不包含于平面EFAD,
∴C1M∥平面EFAD.
(Ⅱ)证明:∵长方体ABCD-A1B1C1D1中,
AD⊥平面AA1B1B,即AD⊥平面B1BAF,
又AD?平面EFAD,
∴平面B1BAF⊥平面EFAD.
(Ⅲ)解:∵AB=AD=2AA1=4,
E是上底面中心,F,M为A1B1与CD的中点,
∴几何体B1EF-BDA的表面积:
S=S梯形ADEF+S梯形BDEB1+S梯形ABB1F+S△B1EF+S△ABD
=
| 1 |
| 2 |
| 7 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=3
| 7 |
| 2 |
点评:本题考查C1M与平面EFAD的位置关系的判断与证明,考查平面与平面垂直的证明,考查几何体B1EF-BDA的表面积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
抛物线y=2x2-12x+19的顶点坐标是( )
| A、(3,1) |
| B、(3,-1) |
| C、(-3,1) |
| D、(-3,-1) |
函数g(x)=2x+5x的零点所在的一个区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(-1,0) |
| D、(-2,-1) |
对于事件A,P(A)表示事件A发生的概率.则下列命题正确的是( )
| A、如果P(A∪B)=P(A)+P(B),那么事件A、B互斥 |
| B、如果P(A∪B)=P(A)+P(B)=1,那么事件A、B对立 |
| C、P(A∪B)=P(A)+P(B)=1是事件A、B对立的充要条件 |
| D、事件A、B互斥是P(A∪B)=P(A)+P(B)的充分不必要条件 |
 已知椭圆E:
已知椭圆E: 已知点A(-3,1)是椭圆
已知点A(-3,1)是椭圆 椭圆C过两个点A(
椭圆C过两个点A(