题目内容
设点P是双曲线
-
=1(a>0,b>0)上任意一点,过点P的直线与两渐近线分别交于P1,P2,设λ=
,求证:S△OP1P2=
ab.
| x2 |
| a2 |
| y2 |
| b2 |
| P1P |
| PP2 |
| (1+λ)2 |
| 4|λ| |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设P(x,y),P1(x1,y1),P2(x2,y2),则y1=
x1,y2=-
x2,依题意,x=
,y=
=
=
•
,将点P(x,y)代入双曲线方程,可得x1x2=
,|OP1|•|OP2|=
,设直线OP1与OP2所成的夹角为2θ,由tanθ=
,进一步可得sin2θ=
=
,从而可证得结论成立.
| b |
| a |
| b |
| a |
| x1+λx2 |
| 1+λ |
| y1+λy2 |
| 1+λ |
| ||||
| 1+λ |
| b |
| a |
| x1-λx2 |
| 1+λ |
| a2(1+λ)2 |
| 4λ |
| c2(1+λ)2 |
| 4|λ| |
| b |
| a |
| 2ab | ||
|
| 2ab |
| c2 |
解答:
证明:设P(x,y),P1(x1,y1),P2(x2,y2),
则y1=
x1,y2=-
x2,∵λ=
,
∴x=
,y=
=
=
•
,
由点P(x,y)在双曲线
-
=1(a>0,b>0)上,
∴
-
=1,
化简得:x1x2=
,
又|OP1|=
=
|x1|,同理可得|OP2|=
|x2|,
∴|OP1|•|OP2|=
|x1|•
|x1|=
•
=
.
设直线OP1与OP2所成的夹角为2θ,∵tanθ=
,
∴tan2θ=
=
=
,
∴sin2θ=
=
,
∴S△OP1P2=
•|OP1|•|OP2|sin2θ=
•
=
ab.
则y1=
| b |
| a |
| b |
| a |
| P1P |
| PP2 |
∴x=
| x1+λx2 |
| 1+λ |
| y1+λy2 |
| 1+λ |
| ||||
| 1+λ |
| b |
| a |
| x1-λx2 |
| 1+λ |
由点P(x,y)在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴
| (x1+λx2)2 |
| a2(1+λ)2 |
| (x1-λx2)2 |
| a2(1+λ)2 |
化简得:x1x2=
| a2(1+λ)2 |
| 4λ |
又|OP1|=
x12+
|
| c |
| a |
| c |
| a |
∴|OP1|•|OP2|=
| c |
| a |
| c |
| a |
| c2 |
| a2 |
| a2(1+λ)2 |
| 4|λ| |
| c2(1+λ)2 |
| 4|λ| |
设直线OP1与OP2所成的夹角为2θ,∵tanθ=
| b |
| a |
∴tan2θ=
| 2tanθ |
| 1-tan2θ |
2×
| ||
1-
|
| 2ab |
| a2-b2 |
∴sin2θ=
| 2ab | ||
|
| 2ab |
| c2 |
∴S△OP1P2=
| 1 |
| 2 |
| 1 |
| 2 |
|
| a2(1+λ)2 |
| 4|λ| |
| 2ab |
| c2 |
| (1+λ)2 |
| 4|λ| |
点评:本题考查双曲线的标准方程与性质的综合应用,考查直线与圆锥曲线的位置关系,求得|OP1|•|OP2|=
与sin2θ=
=
是难点,也是关键,属于难题.
| c2(1+λ)2 |
| 4|λ| |
| 2ab | ||
|
| 2ab |
| c2 |

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知全集U={1,2,3,4,5,6},A∩(CUB)={1,2},A∩B={6},(∁UA)∩(∁UB)={4},则B=( )
| A、{3,6} |
| B、{5,6} |
| C、{3,5} |
| D、{3,5,6} |
曲线y=
与x=1,x=4及x轴所围成的封闭图形的面积为( )
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
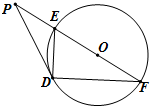 如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4
如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4