题目内容
在平面上,已知
⊥
,|
|=|
|=1,
=
+
,若|
|<
,则|
|的取值范围是( )
| AB1 |
| AB2 |
| OB1 |
| OB2 |
| AP |
| AB1 |
| AB2 |
| OP |
| 1 |
| 2 |
| OA |
A、(0,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
考点:向量的模
专题:平面向量及应用
分析:根据
⊥
,
=
+
,可知:四边形AB1PB2是一个矩形.以AB1,AB2所在直线为坐标轴建立直角坐标系.设|AB1|=a,|AB2|=b.点O的坐标为(x,y),点P(a,b).根据向量的坐标运算、模的计算公式、不等式的性质即可得出.
| AB1 |
| AB2 |
| AP |
| AB1 |
| AB2 |
解答:
解:根据
⊥
,
=
+
,可知:四边形AB1PB2是一个矩形.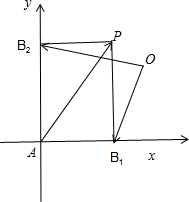
以AB1,AB2所在直线为坐标轴建立直角坐标系.设|AB1|=a,|AB2|=b.
点O的坐标为(x,y),点P(a,b).
∵|
|=|
|=1,
∴
,
变形为
.
∵|
|<
,∴(x-a)2+(y-b)2<
,
∴1-x2+1-y2<
,
∴x2+y2>
.①
∵(x-a)2+y2=1,∴y2≤1.
同理,x2≤1.
∴x2+y2≤2.②
由①②可知:
<x2+y2≤2.
∵|
|=
,
∴
<|
|≤
.
故选:D.
| AB1 |
| AB2 |
| AP |
| AB1 |
| AB2 |

以AB1,AB2所在直线为坐标轴建立直角坐标系.设|AB1|=a,|AB2|=b.
点O的坐标为(x,y),点P(a,b).
∵|
| OB1 |
| OB2 |
∴
|
变形为
|
∵|
| OP |
| 1 |
| 2 |
| 1 |
| 4 |
∴1-x2+1-y2<
| 1 |
| 4 |
∴x2+y2>
| 7 |
| 4 |
∵(x-a)2+y2=1,∴y2≤1.
同理,x2≤1.
∴x2+y2≤2.②
由①②可知:
| 7 |
| 4 |
∵|
| OA |
| x2+y2 |
∴
| ||
| 2 |
| OA |
| 2 |
故选:D.
点评:本题考查了向量的平行四边形法则、矩形的定义、向量的坐标运算、模的计算公式、不等式的性质,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知全集U={1,2,3,4,5,6},A∩(CUB)={1,2},A∩B={6},(∁UA)∩(∁UB)={4},则B=( )
| A、{3,6} |
| B、{5,6} |
| C、{3,5} |
| D、{3,5,6} |
函数y=ax-2(a>0,a≠1)的图象必经过点( )
| A、(0,1) |
| B、(1,1) |
| C、(2,0) |
| D、(2,1) |
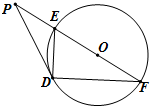 如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4
如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4