题目内容
6.过点M(2,-2p)引抛物线x2=2py(p>0)的切线,切点分别为A,B,若$|{AB}|=4\sqrt{10}$,则p的值是( )| A. | 1或2 | B. | $\sqrt{2}$或2 | C. | 1 | D. | 2 |
分析 求出直线MA,MB的方程,利用韦达定理,结合弦长公式,即可得出结论.
解答 解:由题意设A(x1,y1),B(x2,y2).
由x2=2py得y=$\frac{{x}^{2}}{2p}$,∴y′=$\frac{x}{p}$,
因此直线MA的方程为y+2p=$\frac{{x}_{1}}{p}$(x-2),整理可得x12-4x1-4p2=0,
同理,直线MB的方程为x22-4x2-4p2=0,
所以x1,x2是方程x2-4x-4p2=0的两根,
因此x1+x2=4,x1x2=-4p2,
又kAB=$\frac{{x}_{1}+{x}_{2}}{2p}$=$\frac{2}{p}$.
由弦长公式得|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+\frac{4}{{p}^{2}}}•\sqrt{16+16{p}^{2}}$=4$\sqrt{10}$,
所以p=1或p=2,
故选A.
点评 本题主要考查了直线与圆锥曲线的关系的综合问题.考查了学生分析推理能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
| A. | 6种 | B. | 24种 | C. | 30种 | D. | 36种 |
1.设a∈R,“1,a,16为等比数列”是“a=4”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
11.若将两个顶点在抛物线y2=4x上,另一个顶点是此抛物线焦点的正三角形的个数记为n,则( )
| A. | n=0 | B. | n=1 | C. | n=2 | D. | n≥3 |
15.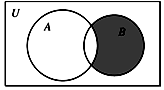 设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )
设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )
 设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )
设全集U=N*,集合A={1,2,3,5},B={2,4,6},则图中的阴影部分表示的集合为( )| A. | {2} | B. | {4,6} | C. | {1,3,5} | D. | {2,4,6} |
16.已知数列{an}的前n项和为Sn,且对任意正整数n都有an=$\frac{3}{4}$Sn+2成立.若bn=log2an,则b1008=( )
| A. | 2017 | B. | 2016 | C. | 2015 | D. | 2014 |