题目内容
定义在R上的奇函数f(x)满足f(x)=f(x+2),且x∈(-1,0)时,f(x)=2x-
,则f(log218)= .
| 1 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:易得函数的周期为2,可得f(log218)=f(log218-4)=f(log2
)=-f(-log2
),代入已知解析式计算可得.
| 9 |
| 8 |
| 9 |
| 8 |
解答:
解:∵函数满足f(x)=f(x+2),∴函数f(x)周期T=2,
∵log218-4=log218-log216=log2
∈(0,1),∴-log2
∈(-1,0),
∴f(log218)=f(log218-4)=f(log2
),
=-f(-log2
)=-2-log2
+
=-
+
=-
,
故答案为:-
.
∵log218-4=log218-log216=log2
| 9 |
| 8 |
| 9 |
| 8 |
∴f(log218)=f(log218-4)=f(log2
| 9 |
| 8 |
=-f(-log2
| 9 |
| 8 |
| 9 |
| 8 |
| 1 |
| 2 |
| 8 |
| 9 |
| 1 |
| 2 |
| 7 |
| 18 |
故答案为:-
| 7 |
| 18 |
点评:本题考查函数的奇偶性和周期性,涉及对数的运算,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
关于直线a、b、c,以及平面M、N,给出下列命题:
①若a∥M,b∥M,则a∥b;
②若a∥M,b⊥M,则a⊥b;
③若a∥b,b∥M,则a∥M;
④若a⊥M,a∥N,则M⊥N,
其中正确命题的个数为( )
①若a∥M,b∥M,则a∥b;
②若a∥M,b⊥M,则a⊥b;
③若a∥b,b∥M,则a∥M;
④若a⊥M,a∥N,则M⊥N,
其中正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
把一颗骰子投掷两次,第一次出现的点数记为m,第二次出现的点数记为n,则3m≠2n的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
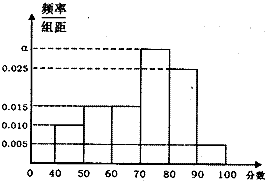 某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.
某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.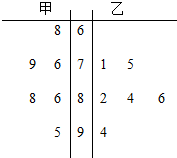 在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图: