题目内容
2.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,且f($\frac{π}{3}$)=1,则f(x)的一个对称中心坐标是( )| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
分析 由函数的周期性可得ω,代入点的坐标可得φ值,可得函数的对称中心,结合选项可得.
解答 解:∵函数f(x)=sin(ωx+φ)的最小正周期为4π,
∴$\frac{2π}{ω}$=4π,解得ω=$\frac{1}{2}$,故f(x)=sin($\frac{1}{2}$x+φ),
再由f($\frac{π}{3}$)=1可得$\frac{1}{2}$×$\frac{π}{3}$+φ=2kπ+$\frac{π}{2}$,k∈Z,
由|φ|<$\frac{π}{2}$可得φ=$\frac{π}{3}$,故f(x)=sin($\frac{1}{2}$x+$\frac{π}{3}$),
由$\frac{1}{2}$x+$\frac{π}{3}$=kπ可得x=2kπ-$\frac{2π}{3}$,k∈Z
∴f(x)的对称中心为(2kπ-$\frac{2π}{3}$,0),k∈Z,
结合选项可知当k=0时,f(x)的一个对称中心为(-$\frac{2π}{3}$,0),
故选:A.
点评 本题考查正弦函数的图象,涉及正弦函数的周期性和对称性,属基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
13.从个位数与十位数之和为偶数的两位数中任取一个,其中个位数为2或3的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
7.运行如图所示的程序框图,则输出的S值为( )
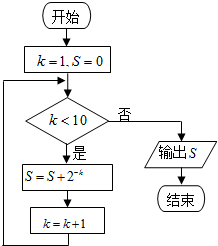

| A. | $\frac{{{2^9}-1}}{2^9}$ | B. | $\frac{{{2^9}+1}}{2^9}$ | C. | $\frac{{{2^{10}}-1}}{{{2^{10}}}}$ | D. | $\frac{{{2^{10}}}}{{{2^{10}}+1}}$ |
14.已知AB为圆x2+y2=1的一条直径,点P为直线x-y+2=0上任意一点,则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |