题目内容
10.已知函数y=sin($ωx+\frac{π}{4}$)(ω>0)是区间[$\frac{3}{4}π$,π]上的增函数,则ω的取值范围是(0,$\frac{3}{4}$].分析 可以通过角的范围[$\frac{3π}{4}$,π],得到(ωx+$\frac{π}{4}$)的取值范围,直接推导ω的范围即可.
解答 解:由于x∈[$\frac{3}{4}$π,π],
故(ωx+$\frac{π}{4}$)∈[$\frac{3π}{4}$ω+$\frac{π}{4}$,πω+$\frac{π}{4}$],
∵函数f(x)=sin(ωx+$\frac{π}{4}$)(ω>0)在[$\frac{3π}{4}$,π]上是增函数,
∴$\left\{\begin{array}{l}{\frac{3π}{4}ω+\frac{π}{4}≥-\frac{π}{2}}\\{πω+\frac{π}{4}≤\frac{π}{2}}\\{ω>0}\end{array}\right.$,
∴0<ω≤$\frac{3}{4}$,
故答案为:(0,$\frac{3}{4}$].
点评 本题考查三角函数的单调性的应用,函数的解析式的求法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,且f($\frac{π}{3}$)=1,则f(x)的一个对称中心坐标是( )
| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
19.已知a,b∈R,则“$\sqrt{a-1}>\sqrt{b-1}$”是“logab<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA是四棱锥P-ABCD的高,PA=AB=2,点M,N,E分别是PD,AD,CD的中点.
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA是四棱锥P-ABCD的高,PA=AB=2,点M,N,E分别是PD,AD,CD的中点.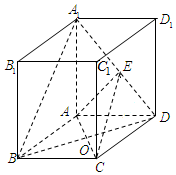 如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.
如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.



