题目内容
14.已知AB为圆x2+y2=1的一条直径,点P为直线x-y+2=0上任意一点,则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
分析 运用向量加减运算和数量积的性质,可得$\overrightarrow{PA}•\overrightarrow{PB}$=($\overrightarrow{PO}$+$\overrightarrow{OA}$)•($\overrightarrow{PO}$+$\overrightarrow{OB}$)=|$\overrightarrow{PO}$|2-r2,即为d2-r2,运用点到直线的距离公式,可得d的最小值,进而得到结论.
解答 解:由$\overrightarrow{PA}•\overrightarrow{PB}$=($\overrightarrow{PO}$+$\overrightarrow{OA}$)•($\overrightarrow{PO}$+$\overrightarrow{OB}$)
=$\overrightarrow{PO}$2+$\overrightarrow{PO}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)+$\overrightarrow{OA}$•$\overrightarrow{OB}$=|$\overrightarrow{PO}$|2-r2,
即为d2-r2,其中d为圆外点到圆心的距离,r为半径,
因此当d取最小值时,$\overrightarrow{PA}•\overrightarrow{PB}$的取值最小,
可知d的最小值为$\frac{|0-0+2|}{\sqrt{2}}$=$\sqrt{2}$,
故$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为2-1=1.
故选:A.
点评 本题考查直线与圆的位置关系以及向量的数量积的运算,注意运用向量的平方即为模的平方,以及点到直线的距离公式,属于中档题.

| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{8}$ | D. | $\frac{11π}{24}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
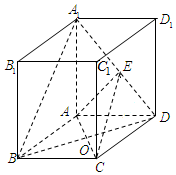 如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.
如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.