题目内容
12．已知sinx+2cosx=$\frac{\sqrt{10}}{2}$．（1）求tan2x的值；
（2）求cos4x-2sinxcosx-sin4x的值．
分析 由条件利用同角三角函数的基本关系，求得要求式子的值．
解答 解：（1）∵sinx+2cosx=$\frac{\sqrt{10}}{2}$，平方可得sin2x+4sinxcosx+4cos2x=$\frac{5}{2}$（sin2x+cos2x），
化简可得3sin2x-8sinxcosx-3cos2x=0，即（sinx-3cosx）•（3sinx+cosx）=0，
∴tanx=3，或tanx=$\frac{1}{3}$，
∴tan2x=$\frac{2tanx}{1{-tan}^{2}x}$=-$\frac{3}{4}$．
（2）cos4x-2sinxcosx-sin4x=（cos2x+sin2x）•（cos2x-sin2x）-2sinxcosx
=cos2x-sin2x-2sinxcosx=$\frac{{cos}^{2}x{-sin}^{2}x-2sinxcosx}{{sin}^{2}x{+cos}^{2}x}$=$\frac{1{-tan}^{2}x-2tanx}{{tan}^{2}x+1}$，
当tanx=3 时，$\frac{1{-tan}^{2}x-2tanx}{{tan}^{2}x+1}$=-$\frac{7}{5}$；
当tanx=$\frac{1}{3}$时，$\frac{1{-tan}^{2}x-2tanx}{{tan}^{2}x+1}$=$\frac{1}{5}$，
故cos4x-2sinxcosx-sin4x的值为-$\frac{7}{5}$或$\frac{1}{5}$．
点评 本题主要考查同角三角的基本关系，属于中档题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
2．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为4π，且f（$\frac{π}{3}$）=1，则f（x）的一个对称中心坐标是（ ）
| A． | （-$\frac{2π}{3}$，0） | B． | （-$\frac{π}{3}$，0） | C． | （$\frac{2π}{3}$，0） | D． | （$\frac{5π}{3}$，0） |
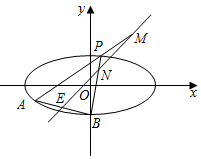如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，（a＞b＞0），点B是其下顶点，直线x+3y+6=0与椭圆C交于A，B两点（点A在x轴下方），且线段AB的中点E在直线y=x上．