题目内容
17.曲线$y=\frac{{3{x^2}+sinx+3}}{{{x^2}+1}}$的对称中心坐标为(0,3).分析 根据函数的图象即可求出.
解答  解:$y=\frac{{3{x^2}+sinx+3}}{{{x^2}+1}}$=3+$\frac{sinx}{{x}^{2}+1}$,
解:$y=\frac{{3{x^2}+sinx+3}}{{{x^2}+1}}$=3+$\frac{sinx}{{x}^{2}+1}$,
当x=0时,$\frac{sinx}{{x}^{2}+1}$=0,
∴函数的对称中心为(0,3).
故答案为:(0,3).
点评 本题考查学生灵活运图象求出对称性的能力,考查合情推理的探究能力和创新精神.

练习册系列答案
相关题目
8.在定义域内既是奇函数又是减函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-x+$\frac{1}{x}$ | ||
| C. | y=-x|x| | D. | y=$\left\{\begin{array}{l}{-x+1,x>0}\\{-x-1,x≤0}\end{array}\right.$ |
2.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,且f($\frac{π}{3}$)=1,则f(x)的一个对称中心坐标是( )
| A. | (-$\frac{2π}{3}$,0) | B. | (-$\frac{π}{3}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{3}$,0) |
9.函数$y=sin(2x-\frac{π}{3})$与$y=cos(2x+\frac{2π}{3})$的图象关于直线x=a对称,则a可能是( )
| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{8}$ | D. | $\frac{11π}{24}$ |
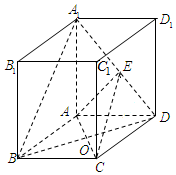 如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.
如图,四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在线段A1D上.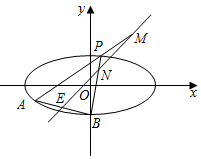 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),点B是其下顶点,直线x+3y+6=0与椭圆C交于A,B两点(点A在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),点B是其下顶点,直线x+3y+6=0与椭圆C交于A,B两点(点A在x轴下方),且线段AB的中点E在直线y=x上.