题目内容
19.在△ABC中,sin2B=sinAsinC.(1)若$\frac{1}{tanA}$,$\frac{\sqrt{3}}{3}$,$\frac{1}{tanC}$成等差数列,求cosB的值;
(2)若$\frac{BC}{sinA}$=4,求△ABC面积的最大值.
分析 (1)根据等差数列的定义以及三角恒等变换求出sinB,从而求出cosB的值即可;
(2)求出三角形的面积的解析式,令f(x)=8sin3x,(0<x<π),根据函数的单调性求出三角形面积的最大值即可.
解答 解:(1))若$\frac{1}{tanA}$,$\frac{\sqrt{3}}{3}$,$\frac{1}{tanC}$成等差数列,
则$\frac{2\sqrt{3}}{3}$=$\frac{cosA}{sinA}$+$\frac{cosC}{sinC}$=$\frac{sinCcosA+cosCsinA}{sinAsinC}$=$\frac{sin(A+C)}{{sin}^{2}B}$=$\frac{1}{sinB}$,
故sinB=$\frac{\sqrt{3}}{2}$,cosB=±$\frac{1}{2}$;
(2)若$\frac{BC}{sinA}$=4,即$\frac{b}{sinB}$=4,b2=16sin2B,
∵sin2B=sinAsinC,
∴ac=b2,
∴S△ABC=$\frac{1}{2}$b2sinB=8sin3B,(0<B<π),
令f(x)=8sin3x,(0<x<π),
则f′(x)=24sin2xcosx,
令f′(x)>0,解得:x<$\frac{π}{2}$,
令f′(x)<0,解得:x>$\frac{π}{2}$,
故f(x)在(0,π)递增,
故f(x)在(0,$\frac{π}{2}$)递增,在($\frac{π}{2}$,π)递减,
f(x)max=f($\frac{π}{2}$)=8,
故三角形面积的最大值是8.
点评 本题考查了正弦定理的应用,考查等差数列以及导数的应用,是一道中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
10.球O的半径为1,该球的一小圆O1上两点A、B的球面距离为$\frac{π}{3}$,OO1=$\frac{\sqrt{2}}{2}$,则∠AO1B=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | π |
7.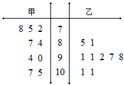 某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
 某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2>s乙2 | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2<s乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2>s乙2 | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2<s乙2 |
4.已知f(x)是定义在R上的偶函数,它在[0,+∞)上递增,那么一定有( )
| A. | $f(\frac{3}{4})<f({a^2}-a+1)$ | B. | $f(\frac{3}{4})≤f({a^2}-a+1)$ | C. | $f(\frac{3}{4})>f({a^2}-a+1)$ | D. | $f(\frac{3}{4})≥f({a^2}-a+1)$ |
9.等差数列{an}和{bn},其前n项和分别为Sn,Tn,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{7n+2}{n+3}$,则$\frac{{{a_{10}}}}{{{b_{10}}}}$等于( )
| A. | $\frac{72}{13}$ | B. | $\frac{135}{22}$ | C. | $\frac{79}{14}$ | D. | $\frac{142}{23}$ |
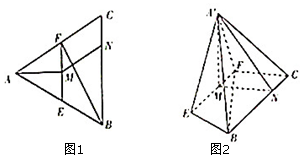 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.