题目内容
10.球O的半径为1,该球的一小圆O1上两点A、B的球面距离为$\frac{π}{3}$,OO1=$\frac{\sqrt{2}}{2}$,则∠AO1B=( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | π |
分析 由题意知应先求出AB的长度,在直角三角形AOB中由余弦定理可得AB=1,由此知三角形AO1B的三边长,由此可以求出∠AO1B的值.
解答 解:由题设知OO1=$\frac{\sqrt{2}}{2}$,OA=OB=1,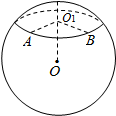
在圆O1中有O1A=O1B=$\frac{\sqrt{2}}{2}$,
又A,B两点间的球面距离为$\frac{π}{3}$,
由余弦定理,得:AB=1,
在三角形AO1B中由勾股定理可得:∠AO1B=$\frac{π}{2}$,
故选:B.
点评 本题的考点是球面距离及相关计算,其考查背景是球内一小圆上两点的球面距,对空间想象能力要求较高,此类题是一个基本题型,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.两个线性相关变量满足如下关系:则y对x的回归方程是( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A. | $\widehat{y}$=0.87x+0.32 | B. | $\widehat{y}$=3.42x-3.97 | C. | $\widehat{y}$═1.23x+0.08 | D. | $\widehat{y}$═2.17x+32.1 |
2.设f(x)是定义在正整数集上的函数,且满足:对于定义域内任意的k,若f(k)≥k2成立,则f(k+1)≥(k+1)2成立.则下列命题正确的是( )
| A. | 若f(3)≥9成立,则对于任意k∈N*,均有f(k)≥k2成立 | |
| B. | 若f(3)≥9成立,则对于任意k≥3,k∈N*,均有f(k)<k2成立 | |
| C. | 若f(3)≥9成立,则对于任意k<3,k∈N*,均有f(k)<k2成立 | |
| D. | 若f(3)=9成立,则对于任意k≥3,k∈N*,均有f(k)≥k2成立 |