题目内容
16．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的数据如下：| 零件的个数x（个） | 2 | 3 | 4 | 5 |
| 加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
分析 根据回归直线方程过样本中心点，即可求出方程系数b的值．
解答 解：∵$\overline{x}$=$\frac{1}{4}$×（2+3+4+5）=3.5，
$\overline{y}$=$\frac{1}{4}$×（2.5+3+4+4.5）=3.5，
回归直线方程y=bx+1.05过样本中心点，
∴3.5b+1.05=3.5，
解得b=0.7．
故答案为：0.7．
点评 本题主要考查了回归方程过样本中心以及平均数的计算问题，是基础题目．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
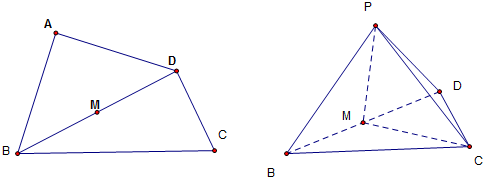
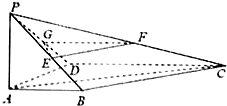已知如图，四边形ABCD是直角梯形，AB∥DC，AB⊥AD，AP⊥平面ABCD，DC=2AB=2AD=2AP，点E、F、G分别是PB、PC、PD的中点．
1．已知某一随机变量ξ的概率分布如下，且E（ξ）=6.3，则a的值为7．
| ξ | 4 | a | 9 |
| P | 0.5 | 0.1 | b |
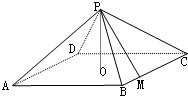如图：四棱锥P-ABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB=2，∠BAD=$\frac{π}{3}$，M是BC上的点，且BM=$\frac{1}{2}$，
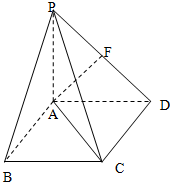如图，四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是边长为2的正方形，PA=AD，F为PD的中点．
6．已知$f（x）=sin[\frac{π}{3}（x+1）]-\sqrt{3}cos[\frac{π}{3}（x+1）]$，则f（1）+f（2）+f（3）+…+f（2013）=（ ）
| A． | -$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | -2$\sqrt{3}$ | D． | 2$\sqrt{3}$ |