题目内容
已知f(x)=loga
(a>0,且a≠1)
(Ⅰ)求函数f(x)的定义域.
(Ⅱ)证明函数f(x)为奇函数.
(Ⅲ)求使f(x)>f(-2)成立的x的取值范围.
| x-1 |
| x+1 |
(Ⅰ)求函数f(x)的定义域.
(Ⅱ)证明函数f(x)为奇函数.
(Ⅲ)求使f(x)>f(-2)成立的x的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(Ⅰ)根据对数中的真数大于0,对于函数f(x)需要
>0,解该不等式便得到定义域.
(Ⅱ)根据奇函数的定义,只需求f(-x),看它和f(x)的关系.
(Ⅲ)根据对数函数的单调性,会得到关于x的不等式,解不等式便得x的取值范围.
| x-1 |
| x+1 |
(Ⅱ)根据奇函数的定义,只需求f(-x),看它和f(x)的关系.
(Ⅲ)根据对数函数的单调性,会得到关于x的不等式,解不等式便得x的取值范围.
解答:
解:(Ⅰ)解
>0得:x>1,或x<-1;
函数f(x)的定义域是{x|x>1,或x<-1}.
(Ⅱ)∵f(-x)=loga
=loga
=loga(
)-1=-loga
;
∴f(-x)=-f(x);
∴函数f(x)为奇函数.
(Ⅲ)若0<a<1,则由f(x)>f(-2)得:loga
>loga3;
0<
<3,解得x<-2,或x>1.
若a>1,则由f(x)>f(-2)得:
>3,解得-2<x<-1.
∴使f(x)>f(-2)成立的x的取值范围是:当0<a<1时是:{x|x<-2,或x>1};
当a>1时是{x|-2<x<-1.
| x-1 |
| x+1 |
函数f(x)的定义域是{x|x>1,或x<-1}.
(Ⅱ)∵f(-x)=loga
| -x-1 |
| -x+1 |
| x+1 |
| x-1 |
| x-1 |
| x+1 |
| x-1 |
| x+1 |
∴f(-x)=-f(x);
∴函数f(x)为奇函数.
(Ⅲ)若0<a<1,则由f(x)>f(-2)得:loga
| x-1 |
| x+1 |
0<
| x-1 |
| x+1 |
若a>1,则由f(x)>f(-2)得:
| x-1 |
| x+1 |
∴使f(x)>f(-2)成立的x的取值范围是:当0<a<1时是:{x|x<-2,或x>1};
当a>1时是{x|-2<x<-1.
点评:理解真数的定义,奇函数的定义,对数函数的单调性,及熟练掌握对数的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一次考试中,五名学生的数学、物理成绩如下表
一次考试中,五名学生的数学、物理成绩如下表
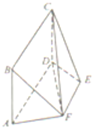 如图,几何体ABCDEF中,四边形ABCD为矩形,且平面ABCD⊥平面ADEF,四边形ADEF为等腰梯形,AD∥EF,AD=2,AB=AF=1,∠DAF=60°.
如图,几何体ABCDEF中,四边形ABCD为矩形,且平面ABCD⊥平面ADEF,四边形ADEF为等腰梯形,AD∥EF,AD=2,AB=AF=1,∠DAF=60°.