题目内容

若关于x的方程-sin2x+sinx+a=0有实数解，则实数a的取值范围是
 
．
考点：三角函数的最值
专题：三角函数的求值
分析：用sinx表示a，进而二次函数的性质和sinx的范围确定a的范围．
解答： 解：对方程等价变换得a=sin2x-sinx=sin2x-sinx+
1
4
-
1
4
=（sinx-
1
2
）2-
1
4
，
∵-1≤sinx≤1，
∴-
1
4
≤a≤2
故答案为：[-
1
4
，2]．
点评：本题主要考查了二次函数的性质，三角函数的最值问题．解题的关键是转化成二次函数的问题，利用二次函数的性质来解决．
练习册系列答案
相关题目
一次考试中，五名学生的数学、物理成绩如下表
学生A1A2A3A4A5
数学8991939597
物理8789899293
（1）要在这五名学生中选2名参加一项活动，求选中的同学中至少有一人的物理成绩高于90分的概率．
（2）请在所给的直角坐标系中画出它们的散点图，并求出这些数据的线性回归直线方程．
参考公式回归直线的方程是：y=bx+a，
其中对应的回归估计值．b=b=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i=1
(xi-
.
x
)2
，a=
.
y
-b
.
x
．
已知数列{an}中，a1=1，a2=0，其前n项和Sn满足：Sn+Sn-2=2Sn-1+2n-1-3（n≥3）
（1）试求数列{an}的通项公式；
（2）求数列{an}的前n项和Sn．
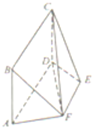如图，几何体ABCDEF中，四边形ABCD为矩形，且平面ABCD⊥平面ADEF，四边形ADEF为等腰梯形，AD∥EF，AD=2，AB=AF=1，∠DAF=60°．
（Ⅰ）证明：AF⊥平面CDF；
（Ⅱ）求几何体ABCDEF的体积．
已知在△ABC中，
a3+b3-c3
a+b-c
=c2，sinA•sinB=
3
4
，则△ABC一定是
 
．
以下四个关于圆锥曲线的命题：
①双曲线
x2
25
-
y2
9
=1与椭圆
x2
35
+y2=1有相同的焦点；
②设A、B为两个定点，k为非零常数，若|
PA
|-|
PB
|=k，则动点P的轨迹为双曲线；
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；
④过定圆C上一定点A作圆的动弦AB，O为坐标原点，若
OP
=
1
2
（
OA
+
OB
），则动点P的轨迹为椭圆．
其中真命题的序号为
 
（写出所有真命题的序号）
给出定义：若n-0.5＜x≤n+0.5（其中n为整数），则n叫做实数x的“友好整数”，记作{x}，即{x}=n，在此基础上给出下列关于函数f（x）=x-{x}的四个命题；
①f（2.4）=-0.6；
②f（-
1
2
）＞f（
1
3
）；
③f（-
1
4
）×f（
1
4
）=f（-
1
16
）；
④y=f（x）的定义域为R，值域是[-
1
2
，
1
2
]；
则其中真命题的序号是
 
．
函数f（x）=x+ex的递增区间是
 
．
210•38+40被25除的余数是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网