题目内容
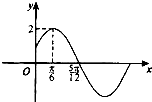 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:直接由图象得到A和T,由周期公式求得ω值,结合五点作图的第三点求φ.
解答:
解:由图可知,A=2,T=4(
-
)=π.
∴ω=
=2.
由五点作图的第三点知,2×
+φ=π,即φ=
.
∴f(x)=2sin(2x+
).
故选:D.
| 5π |
| 12 |
| π |
| 6 |
∴ω=
| 2π |
| π |
由五点作图的第三点知,2×
| 5π |
| 12 |
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
故选:D.
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,关键是掌握由五点作图的某一点求φ,是基础题.

练习册系列答案
相关题目
函数y=ax-2(a>0且a≠1)过定点( )
| A、(1,2) |
| B、(2,1) |
| C、(2,0) |
| D、(0,2) |
若a=20.5,b=logπ3,c=log2sin
,则a,b,c之间的大小关系是( )
| 2π |
| 5 |
| A、c>a>b |
| B、a>b>c |
| C、b>a>c |
| D、b>c>a |
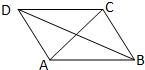 如图平行四边形ABCD中,
如图平行四边形ABCD中,| AC |
| BD |
| AD |
| AC |
| A、1 | B、2 | C、3 | D、4 |
已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x的值为( )


| A、1 | B、-2 |
| C、1或-1 | D、1或-2 |
函数y=
的定义域为( )
| ||
| x-2 |
| A、{x|x≠2} |
| B、{x|x≥0且x≠2} |
| C、{x|x≥0} |
| D、{x|x≥1且x≠2} |
方程lnx+2x-8=0的实数根的个数是( )
| A、0 | B、1 | C、2 | D、3 |
某中学有学生270人(其中一年级108人,二、三年级各81人),将学生按一、二、三年级依次统一编号为1,2,…,270,现考虑选用简单随机抽样、分层抽样和系统抽样三种方案从中抽取10人参加某项调查,如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
| A、②、③都不能为系统抽样 |
| B、②、④都不能为分层抽样 |
| C、③、④都可能为系统抽样 |
| D、①、③都可能为分层抽样 |