题目内容
1.已知半径为r的圆内切于某等边三角形,若在该三角形内任取一点,则该点到圆心的距离大于半径r的概率为( )| A. | $\frac{\sqrt{3}π}{9}$ | B. | 1-$\frac{\sqrt{3}π}{9}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | 1-$\frac{\sqrt{3}π}{18}$ |
分析 半径为r的圆内切于某等边三角形,则等边三角形的边长为2$\sqrt{3}$r,即可求出该点到圆心的距离大于半径r的概率.
解答 解:半径为r的圆内切于某等边三角形,则等边三角形的边长为2$\sqrt{3}$r,
∴该点到圆心的距离大于半径r的概率为1-$\frac{π{r}^{2}}{\frac{\sqrt{3}}{4}×12{r}^{2}}$=1-$\frac{\sqrt{3}}{9}$π,
故选B.
点评 本题考查几何概型,考查面积的计算,属于中档题.

练习册系列答案
相关题目
12.执行如图所示的程序框图,则输出的结果为( )


| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
13.已知复数z满足z($\sqrt{7}$+3i)=16i(i为虚数单位),则复数z的模为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 4 | D. | 8 |
11.对于两条不同的直线m,n和两个不同的平面α,β,以下结论正确的是( )
| A. | 若m?α,n∥β,m,n是异面直线,则α,β相交 | |
| B. | 若m⊥α,m⊥β,n∥α,则n∥β | |
| C. | 若m?α,n∥α,m,n共面于β,则m∥n | |
| D. | 若m⊥α,n⊥β,α,β不平行,则m,n为异面直线 |
 在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证:
在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证: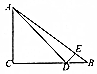 如图,在△ABC中,角A,B,C的对边分别为a,b,c,C=$\frac{π}{2}$,D,E分别为BC,AB上的点,∠ADC=∠EDB=$\frac{π}{4}$,DB=$\sqrt{2}$,AE=3EB,则边长AC的值为$\frac{3\sqrt{2}}{2}$.
如图,在△ABC中,角A,B,C的对边分别为a,b,c,C=$\frac{π}{2}$,D,E分别为BC,AB上的点,∠ADC=∠EDB=$\frac{π}{4}$,DB=$\sqrt{2}$,AE=3EB,则边长AC的值为$\frac{3\sqrt{2}}{2}$.