题目内容
已知函数f(x)=
,则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)是(-∞,+∞)上的增函数 |
| C、f(x)是周期函数 |
| D、f(x)的值域为[-1,+∞) |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:本题根据函数的奇偶性、单调性、周期性去判断函数是否具有奇偶性、单调性、周期性,再研究函数的值域情况不,从而得到本题结论.
解答:
解:选项A,
∵函数f(x)=
,
∴f(1)=14+12=2,
f(-1)=cos(-1)=cos1≠2.
∴f(-x)=f(x).
∴f(x)不是偶函数;
选项B,
当x=-2π时,f(-2π)=cos(-2π)=1,
当x=-π时,f(-π)=cos(-π)=-1,
∵-2π<-π,f(-2π>f(-π),
∴f(x)在(-∞,+∞)上不是增函数;
选项C,
∵f(x)在(0,+∞)是增函数;
∴f(x)不是周期函数;
选项D,
当x>0时,y=x4+x2>0,
当x≤0时,y=cosx∈[-1,1],
∴f(x)的值域为[-1,+∞).
故选D.
∵函数f(x)=
|
∴f(1)=14+12=2,
f(-1)=cos(-1)=cos1≠2.
∴f(-x)=f(x).
∴f(x)不是偶函数;
选项B,
当x=-2π时,f(-2π)=cos(-2π)=1,
当x=-π时,f(-π)=cos(-π)=-1,
∵-2π<-π,f(-2π>f(-π),
∴f(x)在(-∞,+∞)上不是增函数;
选项C,
∵f(x)在(0,+∞)是增函数;
∴f(x)不是周期函数;
选项D,
当x>0时,y=x4+x2>0,
当x≤0时,y=cosx∈[-1,1],
∴f(x)的值域为[-1,+∞).
故选D.
点评:本题考查了奇偶性、单调性、周期性,本题难度不大,属于基础题.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=( )
| A、-1 | B、-3 | C、1 | D、3 |
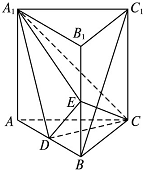 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.