题目内容
已知函数f(x)=3x,f(a+2)=18,g(x)=3ax-4x+1,
(1)求实数a的值;
(2)若ma=1,求g(m)的值;
(3)求函数g(x)在
,
上的最大值和最小值.
(1)求实数a的值;
(2)若ma=1,求g(m)的值;
(3)求函数g(x)在
|
|
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)由已知中f(x)=3x,f(a+2)=18,结合指数的运算性质可得3a=2,化为对数式,可得实数a的值;
(2)若ma=1,则g(m)3-4log23+1,进而根据指数和对数的运算性质得到答案;
(3)g(x)=3ax-4x+1=2x-4x+1,令t=2x,(x∈
,
),则t∈[
,1],则y=g(x)=2x-4x+1=-t2+t+1,进而根据二次函数的图象和性质,得到答案.
(2)若ma=1,则g(m)3-4log23+1,进而根据指数和对数的运算性质得到答案;
(3)g(x)=3ax-4x+1=2x-4x+1,令t=2x,(x∈
|
|
| 1 |
| 4 |
解答:
解:(1)∵f(x)=3x,
∴f(a+2)=3a+2=18,
∴3a=2,
∴a=log32
(2)若ma=1,
则m=log23,
∴g(m)=3-4log23+1=3-9+1=-5,
(3)g(x)=3ax-4x+1=2x-4x+1,
令t=2x,(x∈
,
),则t∈[
,1],
则y=g(x)=2x-4x+1=-t2+t+1的图象是开口朝下,且以直线x=
为对称轴的抛物线,
故当t=
,即x=-1时,函数g(x)取最大值
,
当t=1,即x=0时,函数g(x)取最小值1.
∴f(a+2)=3a+2=18,
∴3a=2,
∴a=log32
(2)若ma=1,
则m=log23,
∴g(m)=3-4log23+1=3-9+1=-5,
(3)g(x)=3ax-4x+1=2x-4x+1,
令t=2x,(x∈
|
|
| 1 |
| 4 |
则y=g(x)=2x-4x+1=-t2+t+1的图象是开口朝下,且以直线x=
| 1 |
| 2 |
故当t=
| 1 |
| 2 |
| 5 |
| 4 |
当t=1,即x=0时,函数g(x)取最小值1.
点评:本题考查的知识点是函数的最值及其几何意义,指数和对数的运算性质,换元法思想,难度中档.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
已知函数f(x)=
,则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)是(-∞,+∞)上的增函数 |
| C、f(x)是周期函数 |
| D、f(x)的值域为[-1,+∞) |
给出下列三个命题:
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线在平面内的射影是一点,则这条直线和这个平面垂直.
其中正确的个数是( )
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线在平面内的射影是一点,则这条直线和这个平面垂直.
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
下列图象中最左边是高青到张店71路公共汽车收支差额y与乘客量x的图象,则图①图②图③的实线所表达的实际意义是( )
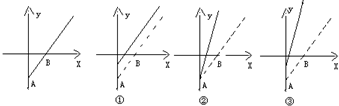

| A、①是票价不变降低成本,②是成本不变提高票价,③是降低成本提高票价 |
| B、①是成本不变提高票价,②是票价不变降低成本,③是降低成本提高票价 |
| C、①是降低成本提高票价,②是票价不变降低成本,③是票价不变降低成本 |
| D、①是成本不变提高票价,②是降低成本提高票价,③是降低成本提高票价 |
已知数列{an}满足:a1=1,an+1=2an+3(n∈N*),则a10=( )
| A、210-3 |
| B、211-3 |
| C、212-3 |
| D、213-3 |
下列命题,能得出直线m与平面α平行的是( )
| A、直线m与平面α内 所有直线平行 |
| B、直线m 与平面α内无数条直线平行 |
| C、直线m与平面α没有公共点 |
| D、直线m与平面α内的一条直线平行 |
函数y=2x-5在R上的单调性是( )
| A、增函数 | B、减函数 |
| C、不增不减 | D、无法确定 |