题目内容
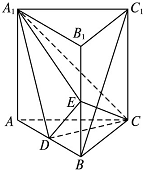 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.(1)证明BC1∥平面A1CD
(2)设AA1=AC=CB=2,AB=2
| 2 |
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结AC1交A1C于点F,连结DF,则BC1∥DF,由此能证明BC1∥平面A1CD.
(2)由已知得AA1⊥CD,CD⊥AB,从而CD⊥平面ABB1A1.由此能求出三菱锥C-A1DE的体积.
(2)由已知得AA1⊥CD,CD⊥AB,从而CD⊥平面ABB1A1.由此能求出三菱锥C-A1DE的体积.
解答:
(1)证明:连结AC1交A1C于点F,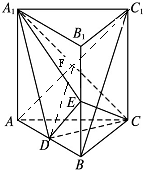
则F为AC1中点又D是AB中点,
连结DF,则BC1∥DF.
因为DF?平面A1CD,BC1不包含于平面A1CD,
所以BC1∥平面A1CD.
(2)解:因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.
由已知AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2
得∠ACB=90°,
CD=
,A1D=
,DE=
,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以三菱锥C-A1DE的体积为:
VC-A1DE=
×
×
×
×
=1.

则F为AC1中点又D是AB中点,
连结DF,则BC1∥DF.
因为DF?平面A1CD,BC1不包含于平面A1CD,
所以BC1∥平面A1CD.
(2)解:因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.
由已知AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2
| 2 |
CD=
| 2 |
| 6 |
| 3 |
故A1D2+DE2=A1E2,即DE⊥A1D.
所以三菱锥C-A1DE的体积为:
VC-A1DE=
| 1 |
| 3 |
| 1 |
| 2 |
| 6 |
| 3 |
| 2 |
点评:本题考查直线与平面平行的证明,考查三菱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,f′(x)<0,且f(2)=-
,则不等式xf(x)<-1的解集为( )
| 1 |
| 2 |
A、(-∞,-
| ||||
B、(-
| ||||
| C、(-∞,-2)∪(2,+∞) | ||||
| D、(-2,2) |
已知函数f(x)=
,则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)是(-∞,+∞)上的增函数 |
| C、f(x)是周期函数 |
| D、f(x)的值域为[-1,+∞) |
 如图所示,已知直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E为BB1的中点,D∈AB,∠A1DE=90°.
如图所示,已知直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E为BB1的中点,D∈AB,∠A1DE=90°.