题目内容
 四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD=
四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD=| 1 |
| 2 |
(1)在侧棱PC上是否存在一点Q,使BQ∥面PAD?说明理由.
(2)求PB与面PCD所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)延长DA交CB延长线于E,连接PE,由已知可得B为EC中点,进而根据Q为CD中点,推断出BQ∥PE,最后利用线面平行的判定定理得出BQ∥PAD
(2)令CD=2a,由VB-PCD=VP-BCD,进而表示出B到面PCD距离,则sinθ的值可得.
(2)令CD=2a,由VB-PCD=VP-BCD,进而表示出B到面PCD距离,则sinθ的值可得.
解答:
解:(1)存在Q为PC中点
证明:延长DA交CB延长线于E,连接PE,
∵AB∥CD,AB=
CD,
∴B为EC中点;
做Q为CP中点,
∴BQ∥PE
又BQ?面PAD,PE?面PAD
∴BQ∥平面PAD
(2)令CD=2a,
VP-BCD=
|PA|•S△DBC=
×a×
×2a×a=
,
∵PA⊥底面ABCD,
∴PA⊥CD,
∵∠ADC=90°
∴CD⊥AD,
∴CD⊥平面PAD,
∴CD⊥PD,
∴PD=
=
a,
设B到面PCD距离为d,
∴S△PDC=
•2a•
a=
a2
由VB-PCD=VP-BCD=
•d•
a2=
∴d=
a,
故sinθ=
=
=
证明:延长DA交CB延长线于E,连接PE,
∵AB∥CD,AB=
| 1 |
| 2 |
∴B为EC中点;
做Q为CP中点,
∴BQ∥PE
又BQ?面PAD,PE?面PAD
∴BQ∥平面PAD
(2)令CD=2a,
VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| a3 |
| 3 |
∵PA⊥底面ABCD,
∴PA⊥CD,
∵∠ADC=90°
∴CD⊥AD,
∴CD⊥平面PAD,
∴CD⊥PD,
∴PD=
| AD2+AP2 |
| 2 |
设B到面PCD距离为d,
∴S△PDC=
| 1 |
| 2 |
| 2 |
| 2 |
由VB-PCD=VP-BCD=
| 1 |
| 3 |
| 2 |
| a3 |
| 3 |
∴d=
| ||
| 2 |
故sinθ=
| d |
| PB |
| ||||
|
| 1 |
| 2 |
点评:本题主要考查了线面平行的判定定理,点到面的距离.考查了学生基础知识的综合运用.

练习册系列答案
相关题目
等比数列{an}前n项和Sn中,S3=-7,S6=-63,那么S9的值是( )
| A、-511 | B、511 |
| C、-1023 | D、1023 |
在R上定义运算|
|=ad-bc,若|
|<|
|成立,则x的取值范围是( )
a b |
c d |
x -x |
3 x |
2 1 |
0 2 |
| A、(-4,1) |
| B、(-1,4) |
| C、(-∞,-4)∪(1,+∞) |
| D、(-∞,-1)∪+∞) |
若不等式ax2+bx+2<0的解集为{x|x<-
或x>
},则
的值为( )
| 1 |
| 3 |
| 1 |
| 2 |
| a-b |
| a |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
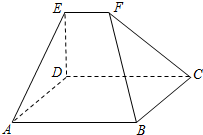 如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.