题目内容
若数列{an}中,a1=
,且对任意的正整数p,q都有ap+q=apaq,则若q=1时,a2+a4+a6+…+a2n+…= .
| 1 |
| 3 |
考点:数列的求和
专题:等差数列与等比数列
分析:对任意的正整数p,q都有ap+q=apaq,a1=
,可得a2=a1a1=
,当q=1时,ap+1=apa1=
ap,可得{an}是首项和公比都为
的等比数列,{a2n}是首项和公比都为
的等比数列,即可得出.
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
解答:
解:∵对任意的正整数p,q都有ap+q=apaq,a1=
,
∴a2=a1a1=
,
若q=1时,ap+1=apa1=
ap,
∴{an}是首项和公比都为
的等比数列,
∴{a2n}是首项和公比都为
的等比数列,
a2+a4+a6+…+a2n+…=
=
.
故答案为:
.
| 1 |
| 3 |
∴a2=a1a1=
| 1 |
| 9 |
若q=1时,ap+1=apa1=
| 1 |
| 3 |
∴{an}是首项和公比都为
| 1 |
| 3 |
∴{a2n}是首项和公比都为
| 1 |
| 9 |
a2+a4+a6+…+a2n+…=
| ||
1-
|
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题考查了等比数列的通项公式及其前n项和公式、数列极限的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
定义在R上的函数f(x)满足:①对任意的x∈R,都有f(1+x)=f(1-x)成立;②对任意的x1,x2∈[1,+∞)且x1≠x2,都有
<0成立,则( )
| f(x1)-f(x2) |
| x1-x2 |
A、f(0)<f(
| ||
B、f(3)<f(
| ||
C、f(3)<f(0)<f(
| ||
D、f(0)<f(3)<f(
|
设函数f(x)(x∈R)满足f(x+1)=-f(x)对任意实数x恒成立,且x∈[0,1]时,f(x)=(x-1)2.那么函数y=f(x)-sinx在区间[0,10]上的零点个数有( )个.
| A、6 | B、7 | C、8 | D、9 |
函数f(x)=|log0.5x|-
的零点个数为( )
| 1 |
| 2x |
| A、1 | B、2 | C、3 | D、4 |
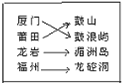 福州、厦门、莆田、龙岩四个城市,它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞,把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分(如图所示是一种“一一对应”的连法,连对的只有一个“厦门→鼓浪屿”).
福州、厦门、莆田、龙岩四个城市,它们分别有一个著名的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞,把福州、厦门、莆田、龙岩四个城市和它们的旅游景点鼓山、鼓浪屿、湄洲岛、龙崆洞分别写成左右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分(如图所示是一种“一一对应”的连法,连对的只有一个“厦门→鼓浪屿”).