题目内容
已知椭圆C1: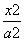 +
+ =1(a>b>0)与双曲线C2:x2-
=1(a>b>0)与双曲线C2:x2-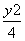 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,若C1恰好将线段AB三等分,则( )
A.a2=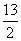 B.a2=13
B.a2=13
C.b2=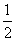 D.b2=2
D.b2=2
C
[解析]

由已知双曲线渐近线为y=±2x.圆方程为x2+y2=a2,则|AB|=2a.不妨取y=2x与椭圆交于P、Q两点,且P在x轴上方,则由已知|PQ|= |AB|=
|AB|= ,∴|OP|=
,∴|OP|= .则点P坐标为(
.则点P坐标为( ,
, ),
),
又∵点P在椭圆上,∴ =1.①
=1.①
又∵a2-b2=5,∴b2=a2-5.②,解①②得
故选C.

练习册系列答案
相关题目
 ,那么k的取值范围是( )
,那么k的取值范围是( )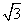 ,+∞) B.[
,+∞) B.[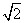 ,+∞)
,+∞) +
+ =1 B.
=1 B. +
+ =1
=1 +
+ =1 D.
=1 D. +
+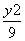 =1
=1 内,向Ω内随机投一点Q,点Q落在椭圆M内的概率为
内,向Ω内随机投一点Q,点Q落在椭圆M内的概率为 ,则椭圆M的方程为________.
,则椭圆M的方程为________. =1的交点为A、B,点P为椭圆上的动点,则使△PAB的面积为
=1的交点为A、B,点P为椭圆上的动点,则使△PAB的面积为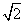 -1的点P的个数为________.
-1的点P的个数为________.