题目内容
11.当x∈(0,+∞)时,函数f(x)=$\frac{x}{e^x}$的值域为$(0,\frac{1}{e}]$.分析 求出原函数的导函数,得到函数在(0,+∞)上的单调性,由此求得函数的值域.
解答 解:由f(x)=$\frac{x}{e^x}$,得f′(x)=$\frac{{e}^{x}-x{e}^{x}}{{e}^{2x}}=\frac{1-x}{{e}^{x}}$,
∴当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0,
∴f(x)(0,1)上为增函数,在(1,+∞)上为减函数,
则f(x)在(0,+∞)上的最大值为f(1)=$\frac{1}{e}$,
又当x→0时f(x)→0,当x→+∞时,f(x)→0,
∴函数f(x)=$\frac{x}{e^x}$的值域为$(0,\frac{1}{e}]$.
故答案为:$(0,\frac{1}{e}]$.
点评 本题考查函数值域的求法,训练了利用导数研究函数的单调性,是中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
2.已知数列{an}的通项公式为an=3n-50,则当n等于( )时,Sn取得最小值?
| A. | 16 | B. | 17 | C. | 18 | D. | 16或17 |
16.已知A(4,0),B(2,2)为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1内的点,M是椭圆上的动点,则|MA|+|MB|的最小值是( )
| A. | 10+2$\sqrt{10}$ | B. | 10+$\sqrt{10}$ | C. | 10-2$\sqrt{10}$ | D. | 10-$\sqrt{10}$ |
3.下列是x和y之间的一组数据
则y关于x的线性回归方程为y=bx+a,对应的直线必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A. | (2,2) | B. | ($\frac{3}{2},2$) | C. | ( $\frac{3}{2},4$) | D. | (1,2) |
20.已知函数f(x)=$\sqrt{3}$sin(2x+$\frac{π}{3}$),其中x∈R,下列结论中正确的是( )
| A. | f(x)是最小正周期为π的偶函数 | |
| B. | f(x)的一条对称轴是 $x=\frac{π}{3}$ | |
| C. | f(x)的最大值为2 | |
| D. | 将函数$y=\sqrt{3}sin2x$的图象向左平移$\frac{π}{6}$个单位得到函数f(x)的图象 |
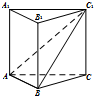 如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.
如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.