题目内容
1.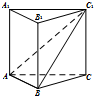 如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.
如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.
分析 连接AC1,BC1,在平面AC1B内过C1作C1D⊥AB于D,连接CD,由题意可得∠C1DC是二面角C1-AB-C的平面角,然后通过求解直角三角形得答案.
解答 解:如图,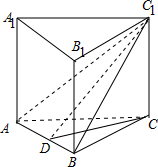
连接AC1,BC1,在平面AC1B内过C1作C1D⊥AB于D,连接CD,
∵三棱柱ABC-A1B1C1的各棱长都相等,且C1C⊥平面ABC,
则AC1=BC1,∴C1D⊥AB,CD⊥AB,
则∠C1DC是二面角C1-AB-C的平面角,
在正三角形ABC中,∵BC=2,BD=1,∴CD=$\sqrt{3}$,
∴tan$∠{C}_{1}CD=\frac{{C}_{1}C}{CD}=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查二面角的平面角的求法,正确找出二面角的平面角是解答此题的关键,是中档题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
16.已知函数f(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$-…+$\frac{{x}^{2013}}{2013}$-$\frac{{x}^{2014}}{2014}$+$\frac{{x}^{2015}}{2015}$,则下列结论正确的是( )
| A. | f(x)在(0,1)上恰有一个零点 | B. | f(x)在(0,1)上恰有两个零点 | ||
| C. | f(x)在(-1,0)上恰有一个零点 | D. | f(x)在(-1,0)上恰有两个零点 |
6.已知函数f(x)=ex(x2+2ax+b)在x=-1处取得极大值t,则t的取值范围是( )
| A. | ($\frac{2}{e}$,+∞) | B. | (-∞,$\frac{2}{e}$) | C. | (-$\frac{2}{e}$,+∞) | D. | (-∞,-$\frac{2}{e}$) |
