题目内容
6.设命题p:曲线y=x2+2x+2t-4与x轴没有交点;命题q:方程$\frac{x^2}{4-t}$+$\frac{y^2}{t-2}$=1所表示的曲线是焦点在x轴的椭圆.(1)若命题p为真命题,求实数t的取值范围;
(2)如果“p∨q”为真命题,“p∧q”为假命题,求实数t的取值范围.
分析 (1)根据二次函数的性质,得到关于t的不等式,解出即可;
(2)求出q为真时t的范围,根据“p∨q”为真命题,“p∧q”为假命题,得到p,q一真一假,从而求出t的范围即可.
解答 解:(1)若p为真命题,
则△=22-4(2t-4)<0,…(2分),
解得$t>\frac{5}{2}$;…(4分)
(2)若命题q:方程$\frac{x^2}{4-t}+\frac{y^2}{t-2}=1$所表示的曲线为焦点在x轴上的椭圆为真,
则有4-t>t-2>0,…(6分)
解得2<t<3.…(8分)
又由题意“p∨q”为真,“p∧q”为假,知命题p与q有且只有一个是正确的,…(10分)
故有:①若p真q假时,则有t≥3;
②若p假q真时,则有$2<t≤\frac{5}{2}$.
综上所述,t的取值范围是$2<t≤\frac{5}{2}$或t≥3.…(14分)
点评 本题考查了二次函数的性质以及椭圆的定义,考查复合命题的判断,是一道中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
16.已知函数f(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$-…+$\frac{{x}^{2013}}{2013}$-$\frac{{x}^{2014}}{2014}$+$\frac{{x}^{2015}}{2015}$,则下列结论正确的是( )
| A. | f(x)在(0,1)上恰有一个零点 | B. | f(x)在(0,1)上恰有两个零点 | ||
| C. | f(x)在(-1,0)上恰有一个零点 | D. | f(x)在(-1,0)上恰有两个零点 |
17.已知函数f(x)=-x3+ax2+bx+c的一个极值点是x=1,则9a+3b的最小值是( )
| A. | 10 | B. | $2\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $4\sqrt{6}$ |
14.已知等差数列{an}中,且a4+a12=10,则前15项和S15=( )
| A. | 15 | B. | 20 | C. | 21 | D. | 75 |
18.如图所示的程序框图中的错误是( )
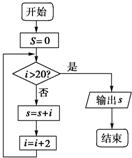

| A. | i没有赋值 | B. | 循环结构有错 | C. | s的计算不对 | D. | 判断条件不成立 |