题目内容
14.已知函数f(x)=|x-a|+|x+b|(a>0,b>0).(Ⅰ)若a=1,b=2,解不等式f(x)≤5;
(Ⅱ)若f(x)的最小值为3,求$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{a}$的最小值.
分析 (Ⅰ)根据绝对值的意义求出x的范围即可;
(Ⅱ)求出a+b的值,根据柯西不等式求出代数式的最小值即可.
解答 解:(Ⅰ)|x-1|+|x+2|≤5,左式可看作数轴上:
点x 到-2 和1 两点的距离之和,…2分
当x=-3 或2 时,距离之和恰为5,
故-3≤x≤2;…5分
(Ⅱ)f(x)=|x-a|+|x+b|≥|x-a-x-b|=a+b,
∴a+b=3,…7分,
由柯西不等式得$(\frac{a^2}{b}+\frac{b^2}{a})(b+a)≥{(a+b)^2}$,
$\therefore$ $\frac{a^2}{b}+\frac{b^2}{a}≥a+b=3$,…9分
当且仅当$a=b=\frac{3}{2}$ 时等号成立,
$\therefore$ $\frac{a^2}{b}+\frac{b^2}{a}$ 的最小值为3.
点评 本题考查了绝对值的意义,考查不等式的性质,是一道中档题.

练习册系列答案
相关题目
9.设a,b,c是三条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )
| A. | 若α⊥β,α⊥γ,则β⊥γ | B. | 若a,b与c所成的角相等,则a∥b | ||
| C. | 若α⊥α,α∥β,则α⊥β | D. | 若a∥b,a?α,则b∥α |
19.已知两定点A(-2,0)和B(2,0),动点P(x,y)在直线l:y=x+4上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
11.已知集合A={x|x2+x-2<0},B={x|2x>1},则A∩(∁UB)=( )
| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |
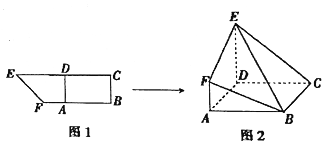 如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列结论错误的是④.(填序号)
如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列结论错误的是④.(填序号)