题目内容
6.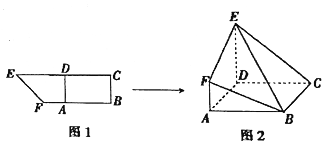 如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列结论错误的是④.(填序号)
如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列结论错误的是④.(填序号)①AC∥平面BEF;
②B、C、E、F四点不可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④直线EF与AC所成角可能为15°.
分析 根据折叠前后线段、角的变化情况,用线面平行、面面垂直的判定定理和性质定理进行判定.
解答 解:对于①,在图2中记AC与BD的交点(中点)为O,取BE的中点为M,连结MO,易证得四边形AOMF为平行四边形,即AC∥FM,∴AC∥平面BEF,故①正确;
对于②,如果四点共面,则Y由BC∥平面ADEF⇒BC∥EF∥AB⇒BC=EF,与已知矛盾,故②正确;
对于③,在梯形ADEF中,易得EF⊥FD,又EF⊥CF,∴EF⊥平面CDF,即有CD⊥EF,∴CD⊥平面ADEF,则平面ADEF⊥平面ABCD,故③正确;
对于④,以D点为原点,DA,DC分别为x,y轴建立空间直角坐标系,利用向量法求直线EF与AC所成角,故④错误.
故答案为:④
点评 本题考查了线面平行、面面垂直的判定定理和性质定理的运用.考查了学生的空间想象能力和推理能力.属于基础题.

练习册系列答案
相关题目
16.下面进位制之间转化错误的是( )
| A. | 31(4)=62(2) | B. | 101(2)=5(10) | C. | 119(10)=315(6) | D. | 27(8)=212(3) |
17.三个互不重合的平面,最多能把空间分成n部分,n的值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
11.已知向量$\overrightarrow a$与向量$\overrightarrow b$满足|$\overrightarrow a$|=3,|$\overrightarrow b$|=2,|$2\overrightarrow a+\overrightarrow b$|=2$\sqrt{13}$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
18.已知$\overrightarrow a$=(sin(x+$\frac{π}{3}$),sin(x-$\frac{π}{6}$)),$\overrightarrow b$=(cos(x-$\frac{π}{6}$),cos(x+$\frac{π}{3}$)),$\overrightarrow a$•$\overrightarrow b$=$\frac{5}{13}$,且x∈[-$\frac{π}{3}$,$\frac{π}{6}$],则sin2x的值为( )
| A. | $\frac{{5\sqrt{3}+12}}{26}$ | B. | $\frac{{5\sqrt{3}-12}}{26}$ | C. | $\frac{{5+12\sqrt{3}}}{26}$ | D. | $\frac{{5-12\sqrt{3}}}{26}$ |