题目内容
求已知函数f(x)=(ax+1)ex的单调区间.
考点:利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:由题意求导f′(x)=(ax+a+1)ex,讨论a以确定导数的正负,从而求函数的单调区间.
解答:
解:∵f(x)=(ax+1)ex,
∴f′(x)=(ax+a+1)ex,
①当a=0时,f(x)在R上是增函数;
②当a<0时,x>-
时,f′(x)<0,
x<-
时,f′(x)>0,
f(x)的单调增区间为(-∞,-
),
单调减区间为(-
,+∞);
③当a>0时,x>-
时,f′(x)>0,
x<-
时,f′(x)<0,
f(x)的单调增区间为(-
,+∞),
单调减区间为(-∞,-
).
∴f′(x)=(ax+a+1)ex,
①当a=0时,f(x)在R上是增函数;
②当a<0时,x>-
| a+1 |
| a |
x<-
| a+1 |
| a |
f(x)的单调增区间为(-∞,-
| a+1 |
| a |
单调减区间为(-
| a+1 |
| a |
③当a>0时,x>-
| a+1 |
| a |
x<-
| a+1 |
| a |
f(x)的单调增区间为(-
| a+1 |
| a |
单调减区间为(-∞,-
| a+1 |
| a |
点评:本题考查了利用导数求函数的单调区间,注意分类讨论,属于中档题.

练习册系列答案
相关题目
 如图所示,已知三棱锥P-ABC中,∠ACB=90°,BC=4,AB=20,D为AB的中点,且△PDB是等边三角形,PA⊥PC.
如图所示,已知三棱锥P-ABC中,∠ACB=90°,BC=4,AB=20,D为AB的中点,且△PDB是等边三角形,PA⊥PC. 已知:如图,点B是AD的中点,点E是AB的中点,AB=AC.求证:CE=
已知:如图,点B是AD的中点,点E是AB的中点,AB=AC.求证:CE=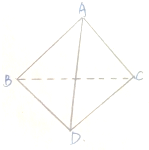 如图,三棱锥A-BCD中,DC⊥BC,BC=2
如图,三棱锥A-BCD中,DC⊥BC,BC=2