题目内容
 已知:如图,点B是AD的中点,点E是AB的中点,AB=AC.求证:CE=
已知:如图,点B是AD的中点,点E是AB的中点,AB=AC.求证:CE=| 1 |
| 2 |
考点:相似三角形的判定
专题:立体几何
分析:利用已知可证△ACE∽△ADC,即可证明.
解答:
证明:∵AB=AC,点B是AD的中点,点E是AB的中点,
∴AE=
AC,AC=
AD.
在△ACE与△ADC中,
=
=
,∠A公用,
∴△ACE∽△ADC,
∴
=
=
,
∴CE=
CD.
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
在△ACE与△ADC中,
| AE |
| AC |
| AC |
| AD |
| 1 |
| 2 |
∴△ACE∽△ADC,
∴
| CE |
| CD |
| AC |
| AD |
| 1 |
| 2 |
∴CE=
| 1 |
| 2 |
点评:本题考查了相似三角形的判定、中点的应用,考查了推理能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=
x+lnx的零点所在的区间是( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知四边形ABCD是平行四边形,点O是空间任意一点,设
=
,
=
,
=
,则向量
用
、
、
表示为( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
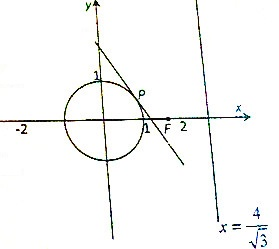 已知动点M到点F(
已知动点M到点F( 如图,在四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,DC⊥BC,求证:平面ABD⊥平面ACD.
如图,在四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,DC⊥BC,求证:平面ABD⊥平面ACD. 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,AD=