题目内容
化简：
．
| (sin2α+cos2α-1)(sin2α-cos2α+1) |
| sin4α |
考点：三角函数中的恒等变换应用,二倍角的正弦
专题：三角函数的求值
分析：先利用平方差公式把分母展开，利用二倍角公式把分母展开，化简整理后，继续用二倍角公式化简约分即可．
解答：
解：原式=
=
=
=
=
=cotα．
| sin22α-(cos2α-1)2 |
| sin4α |
| 1-2cos22α+2cos2α-1 |
| 2sin2αcos2α |
| cos2α(cos2α-1) |
| sin2αcos2α |
| cos2α-1 |
| sin2α |
| 2cos2α+1-1 |
| 2sinαcosα |
点评：本题主要考查了三角函数恒等变换的应用．解题过程中灵活运用二倍角公式，化简的关键是消掉常数项．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
在直角△ABC中，∠BCA=90°，CA=CB=1，设
=λ
，
=λ
（λ∈R），则
•
的最小值为（ ）
| AP |
| AB |
| CQ |
| CB |
| CP |
| AQ |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知数列{an}为等比数列，且a1=1，a4=8，则公比q=（ ）
| A、1 | B、2 | C、4 | D、8 |
如图，在平行四边形ABCD中，AB=2AD，∠BAD=60°，E为AB的中点，将△ADE沿直线DE折起到△PDE的位置，使平面PDE⊥平面BCDE．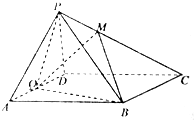
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，点Q为线段AD中点，PQ与QB不垂直．