题目内容
已知数列{an}为等比数列，且a1=1，a4=8，则公比q=（ ）
| A、1 | B、2 | C、4 | D、8 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：利用等比数列的通项公式求解．
解答：
解：∵数列{an}为等比数列，且a1=1，a4=8，
∴1×q3=8，
解得公比q=2．
故选：B．
∴1×q3=8，
解得公比q=2．
故选：B．
点评：本题考查等比数列的公比的求法，是基础题，解题时要注意等比数列的通项公式的求法．
练习册系列答案
名校课堂系列答案
相关题目
已知双曲线
-y2=1（a＞0）的实轴长为2，则该双曲线的离心率为（ ）
| x2 |
| a2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若关于x的不等式x2-x+a＞0恒成立，则a的取值范围为（ ）
A、[
| ||
B、（
| ||
C、（-∞，
| ||
D、（-∞，
|
若执行如图所示的程序框图，当输入n=1，m=5，则输出p的值为（ ）
| A、-4 | B、1 | C、2 | D、5 |
在样本的频率分布直方图中，共有8个小长方形，若最后一个小长方形的面积等于其它7个小长方形的面积和的
，且样本容量为200，则第8组的频数为（ ）
| 1 |
| 4 |
| A、40 | B、0.2 |
| C、50 | D、0.25 |
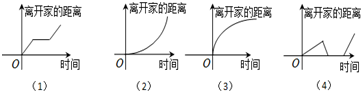
下列所给4个图象中，与所给3件事吻合最好的顺序为（ ）
（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；
（2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．
（1）（2）（3）（4）时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离
（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；
（2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．
（1）（2）（3）（4）时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离
| A、（1）（2）（4） |
| B、（4）（2）（3） |
| C、（4）（1）（3） |
| D、（4）（1）（2） |
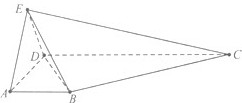如图所示，在四棱锥E-ABCD中，AB∥CD，∠ADC=90°，CD=3，AB=1，EA=AD=DE=2，EC=
按规定：车辆驾驶员血液酒精浓度在20～80mg/100mL（不含80）之间．属酒后驾车：在800mg/100mL（含80）以上时，属醉酒驾车．某市交警在某路段的一次拦查行动中，依法检查了250辆机动车，查处酒后驾车的驾驶员20人，如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图．