题目内容
 如图,在平行四边形ABCD中,AB=2AD,∠BAD=60°,E为AB的中点,将△ADE沿直线DE折起到△PDE的位置,使平面PDE⊥平面BCDE.
如图,在平行四边形ABCD中,AB=2AD,∠BAD=60°,E为AB的中点,将△ADE沿直线DE折起到△PDE的位置,使平面PDE⊥平面BCDE.(Ⅰ)证明:平面PCE⊥平面PDE;
(Ⅱ)设F、M分别为PC、DE的中点,求直线MF与平面PDE所成的角.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)通过证明CE⊥平面PDE,即可证明:平面PCE⊥平面PDE;
(Ⅱ)取PE中点G,连接FG,连接MG,则∠FMG为直线MF与平面PDE所成的角,求出FG,MG,即可求直线MF与平面PDE所成的角.
(Ⅱ)取PE中点G,连接FG,连接MG,则∠FMG为直线MF与平面PDE所成的角,求出FG,MG,即可求直线MF与平面PDE所成的角.
解答:
 (Ⅰ)证明:∵AB=2AD,E为AB的中点,
(Ⅰ)证明:∵AB=2AD,E为AB的中点,
∴AE=AD,
∴∠BAD=60°,
∴△ADE为正三角形,
∴∠AED=60°,
∵BE=BC,∠CBE=120°,
∴∠CEB=30°,
∴CE⊥DE,
∵平面PDE⊥平面BCDE,平面PDE∩平面BCDE=DE,
∴CE⊥平面PDE,
∴平面PCE⊥平面PDE;
(Ⅱ)解:取PE中点G,连接FG,则
∵F为PC的中点,
∴FG∥CE,
∴FG⊥平面PDE,
连接MG,则∠FMG为直线MF与平面PDE所成的角.
设AD=2,则GM=
PD=1,
在△BCE中,BE=BC=2,∠CBE=120°,则
CE2=4+4-2•2•2cos120°=12,∴CE=2
,
∴FG=
.
在直角△FGM中,tan∠FMG=
=
,
∴∠FMG=60°,
∴直线MF与平面PDE所成的角为60°.
 (Ⅰ)证明:∵AB=2AD,E为AB的中点,
(Ⅰ)证明:∵AB=2AD,E为AB的中点,∴AE=AD,
∴∠BAD=60°,
∴△ADE为正三角形,
∴∠AED=60°,
∵BE=BC,∠CBE=120°,
∴∠CEB=30°,
∴CE⊥DE,
∵平面PDE⊥平面BCDE,平面PDE∩平面BCDE=DE,
∴CE⊥平面PDE,
∴平面PCE⊥平面PDE;
(Ⅱ)解:取PE中点G,连接FG,则
∵F为PC的中点,
∴FG∥CE,
∴FG⊥平面PDE,
连接MG,则∠FMG为直线MF与平面PDE所成的角.
设AD=2,则GM=
| 1 |
| 2 |
在△BCE中,BE=BC=2,∠CBE=120°,则
CE2=4+4-2•2•2cos120°=12,∴CE=2
| 3 |
∴FG=
| 3 |
在直角△FGM中,tan∠FMG=
| FG |
| GM |
| 3 |
∴∠FMG=60°,
∴直线MF与平面PDE所成的角为60°.
点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知f(x)=π(x∈R),则f(π2)=( )
| A、π2 | ||
| B、π | ||
C、
| ||
| D、不确定 |
在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其它7个小长方形的面积和的
,且样本容量为200,则第8组的频数为( )
| 1 |
| 4 |
| A、40 | B、0.2 |
| C、50 | D、0.25 |
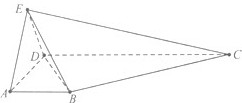 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC= 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示) 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,CD⊥平面PAD,点O,E分别是AD,PC的中点,已知PA=PD,PO=AD=2BC=2CD=2.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,CD⊥平面PAD,点O,E分别是AD,PC的中点,已知PA=PD,PO=AD=2BC=2CD=2.