题目内容
设函数f(x)=|2x+3|.
(Ⅰ)解不等式f(x)<2;
(Ⅱ)若f(x)+2|x-5|>m对一切实数x均成立,求m的取值范围.
(Ⅰ)解不等式f(x)<2;
(Ⅱ)若f(x)+2|x-5|>m对一切实数x均成立,求m的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)利用绝对值不等式的几何意义,解不等式|2x+3|<2即可;
(Ⅱ)依题意,m<[f(x)+2|x-5|]min,利用绝对值三角不等式易求[f(x)+2|x-5|]min=13,从而可得答案.
(Ⅱ)依题意,m<[f(x)+2|x-5|]min,利用绝对值三角不等式易求[f(x)+2|x-5|]min=13,从而可得答案.
解答:
解:(Ⅰ) f(x)<2,即|2x+3|<2
∴-2<2x+3<2,解得:-
<x<-
.
∴原不等式的解集为(-
,-
)(5分)
(Ⅱ)∵f(x)+2|x-5|>m对一切实数x均成立,
∴m<[f(x)+2|x-5|]min,
∵f(x)+2|x-5|=|2x+3|+2|x-5|=|2x+3|+|2x-10|≥|(2x+3)-(2x-10)|=13,
即[f(x)+2|x-5|]min=13,
∴m<13.(10分)
∴-2<2x+3<2,解得:-
| 5 |
| 2 |
| 1 |
| 2 |
∴原不等式的解集为(-
| 5 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵f(x)+2|x-5|>m对一切实数x均成立,
∴m<[f(x)+2|x-5|]min,
∵f(x)+2|x-5|=|2x+3|+2|x-5|=|2x+3|+|2x-10|≥|(2x+3)-(2x-10)|=13,
即[f(x)+2|x-5|]min=13,
∴m<13.(10分)
点评:本题考查绝对值不等式的解法,突出考查绝对值不等式的几何意义与绝对值三角不等式的应用,考查考查化归思想与恒成立问题,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
若执行如图所示的程序框图,当输入n=1,m=5,则输出p的值为( )


| A、-4 | B、1 | C、2 | D、5 |
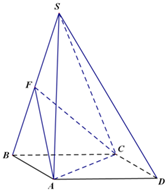 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2 按规定:车辆驾驶员血液酒精浓度在20~80mg/100mL(不含80)之间.属酒后驾车:在800mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查处酒后驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
按规定:车辆驾驶员血液酒精浓度在20~80mg/100mL(不含80)之间.属酒后驾车:在800mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查处酒后驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.