题目内容
已知函数f(x)=
-lnx(a∈R).
(1)当0<a<
时,讨论f(x)的单调性;
(2)设g(x)=x2-2bx+4,当a=
时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)+g(x2)≤0,求实数b的取值范围.
| a(x2+1)+x-1 |
| x |
(1)当0<a<
| 1 |
| 2 |
(2)设g(x)=x2-2bx+4,当a=
| 1 |
| 3 |
考点:利用导数研究函数的单调性
专题:函数的性质及应用
分析:(1)直接利用函数与导数的关系,求出函数的导数,再讨论函数的单调性;
(2)利用导数求出f(x)的最小值、利用二次函数知识或分离常数法求出g(x)在闭区间[1,2]上的最大值,然后解不等式求参数.
(2)利用导数求出f(x)的最小值、利用二次函数知识或分离常数法求出g(x)在闭区间[1,2]上的最大值,然后解不等式求参数.
解答:
解(1)∵f(x)=
-lnx
当
>1时,即0<a<
时,此时f(x)的单调性如下:
当0<a<
时时,f(x)在(0,1),(
,+∞)上是增函数,
在(1,
)上是减函数.
(2)由(1)知,当a=
时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
于是x1∈(0,2)时,f(x1)∈(-∞,
].
存在x2∈[1,2],从而存在使g(x2)=x2-2bx+4≤
-2bx2+4≤[-f(x1)]min=-
,[g(x)]min≤-
,x∈[1,2],
考察g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]最小值.
①当b≤1时,g(x)在[1,2]上递增,[g(x)]min=g(1)=5-2b≤-
,b≥
(舍去),
②当b≥2时,g(x)在[1,2]上递减,[g(x)]min=g(2)=8-4b≤-
,b≥
,
∴b≥
,
③当1<b<2时,g(x)min=g(b)=4-b2≤
,无解.
综上b≥
.
| a(x2+1)+x-1 |
| x |
当
| 1-a |
| a |
| 1 |
| 2 |
| x | (0,1) | 1 | (1,
|
| (
| ||||||
| f′(x) | + | 0 | _ | 0 | + | ||||||
| f(x) | 增 | 减 | 增 |
| 1 |
| 2 |
| 1-a |
| a |
在(1,
| 1-a |
| a |
(2)由(1)知,当a=
| 1 |
| 3 |
于是x1∈(0,2)时,f(x1)∈(-∞,
| 2 |
| 3 |
存在x2∈[1,2],从而存在使g(x2)=x2-2bx+4≤
| x | 2 2 |
| 2 |
| 3 |
| 2 |
| 3 |
考察g(x)=x2-2bx+4=(x-b)2+4-b2,x∈[1,2]最小值.
①当b≤1时,g(x)在[1,2]上递增,[g(x)]min=g(1)=5-2b≤-
| 2 |
| 3 |
| 17 |
| 6 |
②当b≥2时,g(x)在[1,2]上递减,[g(x)]min=g(2)=8-4b≤-
| 2 |
| 3 |
| 13 |
| 6 |
∴b≥
| 13 |
| 6 |
③当1<b<2时,g(x)min=g(b)=4-b2≤
| 2 |
| 3 |
综上b≥
| 13 |
| 6 |
点评:本题将导数、二次函数、不等式知识有机的结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力.

练习册系列答案
相关题目
先后抛掷红、蓝两枚骰子,事件A:红骰子出现3点,事件B:蓝骰子出现的点数为奇数,则P(A|B)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
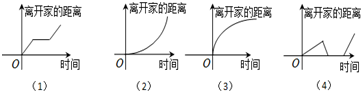
下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离

| A、(1)(2)(4) |
| B、(4)(2)(3) |
| C、(4)(1)(3) |
| D、(4)(1)(2) |
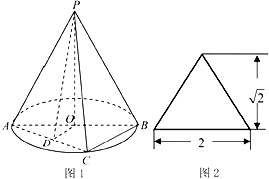 圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点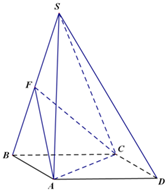 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2